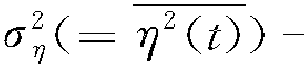斯托克斯理论作了这样的一个假定，在假定波浪运动基本方程的解答可以用一个小参数ε的幂级数展开形式表达式，小参数ε波动特征有关的无因次常数，最有效的波动特征值在水深较大时为H/L，在水深较小时为H/d，因此在幂级数展开式中所取级数的项数愈多，接近于实际的波动特性就愈好。对于更高阶的理论如Stokes二至五阶理论，波高轮廓表示为[2]
这里对于第一，二阶，A=H/2;对于更高的阶数，A小于H/2，是波长和水深的特殊函数。线性理论包括其第一项，高阶Stokes定理包括对应的高阶部分。例如，Stokes二阶定理使用前两项，Stokes五阶定理使用前五项。Stokes波除了波高相对于波长不可视为无限小这一 ...... （共928字） [阅读本文]>>
海洋平台随机动力响应分析及智能控制1.2.1 海洋平台结构振动控制研究的意义随着人类对油气资源的需求日益扩大以及陆上油气资源的逐步枯竭，海上油气资源的开发正越来越受到各国的重视。作为海洋油气资源开发的基础性设施，海洋平台的数量急剧增加
海洋平台随机动力响应分析及智能控制线性波又称小振幅波，是一种简化的最简单的波动，其水面呈现简谐形式的起伏，水质点以固定的圆频率做简谐运动，同时波形以一定的波速c向前传递，波浪中线与静水面重合。虽然海洋中实际发生的波动都不能用这种简单的
海洋平台随机动力响应分析及智能控制海洋中的波浪是随机的，具有统计规律，可以利用概率统计理论进行研究，利用概率统计理论研究海浪现象的理论称为随机波浪理论。随机过程理论告诉我们，当一个随机过程的统计特性不随时间的迁移而变化(或者说，其统计
海洋平台随机动力响应分析及智能控制2.4.1 Morison方程作用于海洋结构物上的随机波浪荷载的计算是非常困难的。因为它包括了波浪和结构物之间的相互作用关系。就随机波浪的本质而言，目前高阶非线性理论发展仍不完备，直到目前为止，与波长
海洋平台随机动力响应分析及智能控制1)动力响应试验结果及分析规则波的试验结果以R01工况(波高0.2 m，周期1.5s，浪向X)为例，位移响应、速度响应及测点1的加速度响应测试结果如图9-21～图9-26所示。图9-21 X方向位移响
上一篇