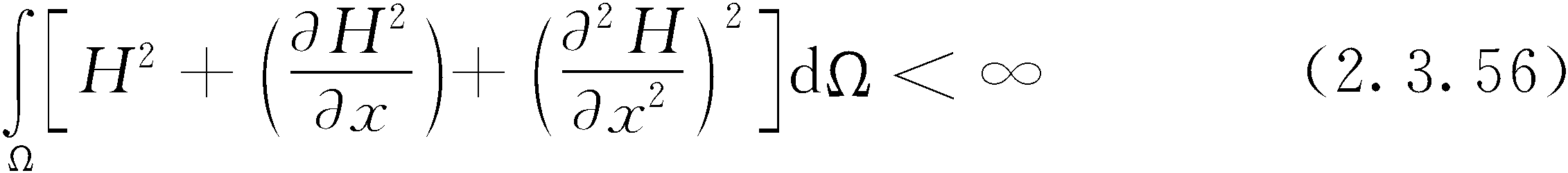
2.3.3小节中推导出了一个含水层流动的二维数学模型。方程的最终形式式 (2.3.50) 包括外部源项的补给，为地下水位的线性函数。该方程的微分形式为
式中： L(H) 为未知水头H (表示潜水层的地下水位和承压含水层的水头) 的函数。这个方程的解析解只有在各向同性的含水层中，并且边界几何形状简单的特殊情况下才能得到。但是，大多数的实际工程问题涉及非均质含水层和不规则几何边界，必须使用数值方法求解式 (2.3.53)。GROW使用有限元方法 (FEM) 求解这个方程。同有限差分法 (有限体积法) 相比 (例如，MODFLOW中所采用的求解方法)，有限元法具有的一个潜在优势是能够用有限元网格来表示复杂的含水层 ...... （共4593字） [阅读本文]>>
城市地下水管理高级仿真与建模世界人口正以惊人的速度增加，增加的人口大部分出现在城市地区 (见图1.1) (联合国，2005)。从1990年到世纪之交，全球人口增长了15% (从53亿到61亿)。而城市地区的人口增长了24%，已达
城市地下水管理高级仿真与建模城市主要地质单位的分布未受到城市发展的影响。然而，少数情况下，城市发展会影响浅层地下物质的分布。· 人工填地： 这些土层可以覆盖城市区域的一大部分，影响地下水流和地下水化学性质。“填地” 或 “填”
城市地下水管理高级仿真与建模城市发展往往对含水层补给有着深刻的影响。影响因素包括地面覆盖的改变程度、高密度的饮用水和污水处理系统、向地下有意识和无意识地高密度污水排放、抽水井过于密集导致的渗透。鉴于一个城市复杂的土地覆盖情况 (
城市地下水管理高级仿真与建模城市地下含水层容易出现水质问题，特别是因为城市产生大量的废弃物，其中一些物质不可避免地进入地下水系统。下文将简要概括了一些主要问题。· 大气以及降水的化学性质： 发电、工业和车辆向大气的排放，会导致大
城市地下水管理高级仿真与建模直到最近为止，模拟城市地下水系统问题的解决方案，仍然要么是使用可用的地下水流动和运移模型，并调整城市数据以满足建模要求，即 “合适” 的方法; 要么是开发独立的城市供水系统或城市水系统组件模型并将这些
上一篇