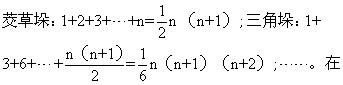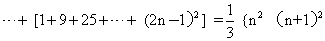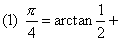一卷。清华蘅芳 (详见《代数术》)撰。《数根术解》是研究初等数论中素数理论及应用问题的专著。华蘅芳列举了 “减数增乘之诸尖堆 (即Cnk)”及“诸乘尖堆 (即Cn+k-1k)n说明连续k个自然数之积必可被k!整除，他还研究了一些组合数的性质并得到若干公式，证明了当p为素数时有： p|2p-2，这是费马定理一特例，在1872年李善兰《考数根法》中已给出了一个证明，华蘅芳的证法与十八世纪瑞士著名数学家欧拉(1707—1783)的证明基本一致。华蘅芳的工作没有超出前人之处。《数根术解》版本有《行素轩算稿》本;《测海山房丛刻》本;《中西算学汇通》本 ...... （共278字） [阅读本文]>>
四库一卷。明徐孝编、张元善校。徐孝，明末顺天(今北京市)人，不仕。著《合并字学集篇集韵》二十三卷，《重订司马温公等韵图经》即是书所附之韵表。张元善永城(今河南永城县)人，彭城伯骐之后，袭封惠安伯。张氏卒于万
四库八卷。元丁巨(生卒年不详)撰。丁巨始末未详，在《丁巨算法》自序中，丁巨记载了成书经过：“独余幼贱，不伍时流，经籍之余事。法物度轨，则间尝用心。因于算术上自九章，下至小法，数十百家，摘取要略。述算法八卷。
四库一卷。清陈世仁(1676—1722)撰。陈世仁字元之，号焕吾，浙江海宁人，系陈訏的族侄，好学工为文，精晓算学。康熙五十四年(1715)以进士入翰林后，即回乡不仕。《少广补遗》专论垛积之术，视垛积为少广，
四库三卷。清邹伯奇(1819—1869)撰。邹伯奇，字特夫，又字一鹗，广东南海人，通经博古，尤擅算学，与夏鸾翔、丁取忠等名家交往甚密，在南方沿海诸省颇负盛名。曾于1866和1868年两度被朝廷召任北京同文馆
四库一卷。清曾纪鸿(1848—1877)撰。曾纪鸿，字栗诚，湖南湘乡人，曾国藩次子，丁取忠的学生，曾与黄宗宪、左潜于丁取忠指导下在长沙古荷花池的白芙堂共同研究数学。与丁取忠等同撰《粟布演草》第一卷、《对数详
上一篇