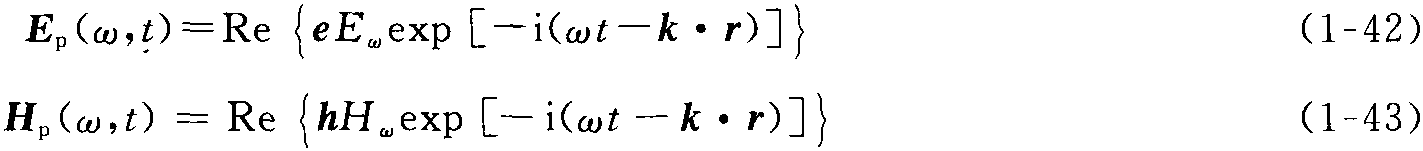在考虑色散、非均匀或者各向异性介质中的传输时，介电张量和磁导率都不能认为是常数，而是与位置和方向相关的函数。对于无增益、无损耗的非均匀、非铁磁介质，麦克斯韦方程组是
式中第二式可写为对方程两边分别作旋量运算，有利用▽×▽×E=▽(▽·E)-▽2E，再考虑(1-37)式中的第三式：▽·εE=ε▽·E+E·▽ε=0，于是得到非均匀介质中的波动方程为其中如果介质的介电常数ε(r)是缓变的，在一个波长范围内可以认为是常数，则(1-40)式的第三项可以忽略，v(r)表示光在介质中的速度受到介质折射率变化的调制 ...... （共292字） [阅读本文]>>
光学目前光学领域内遇到的绝大部分现象和技术，都能从电磁光学得到很好的解释。描述光和物质相互作用的经典理论、半经典理论，均把光辐射视为经典电磁波，遵从光的电磁理论。在整个电磁频谱中，可见光只占很小一部分。由表
光学在国际单位制的体系下，麦克斯韦方程组有最简单的形式：式中，H(r，t)是磁场强度矢量(magneticfieldvector，单位：A/m)，E(r，t)是电场强度矢量(electricfieldvec
光学磁感应强度矢量的散度等于0，这表示它本身是由矢量的旋度产生的。因为对于任意矢量都有：▽·(▽×A)=0，所以，(1-4)式表示有矢量势的存在，令B=▽×A(1-18)A(r，t)是矢量势(vectorp
光学波动方程首先研究没有场源存在的介质中电磁波的传播。在线性、非色散、均匀和各向同性的介质中，假定介质中不存在电流、空间电荷，不考虑铁磁性，也不考虑电极化的高阶项。这时，麦克斯韦方程组变成式中，介电常数和磁
光学场的概念，本质上是非局域的。就是说，所有光学场共享一个空间，而这个空间是由性质不同的介质分布充满的。共享的概念不是简单的数学相加，而是相干叠加，相位和相位分布起着相当重要的作用。电磁光学的基本任务，就是
上一篇