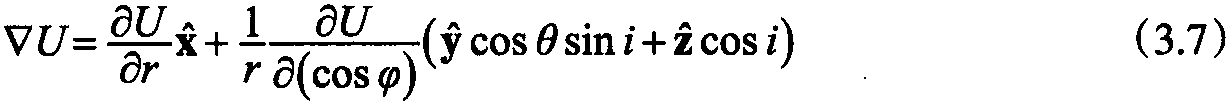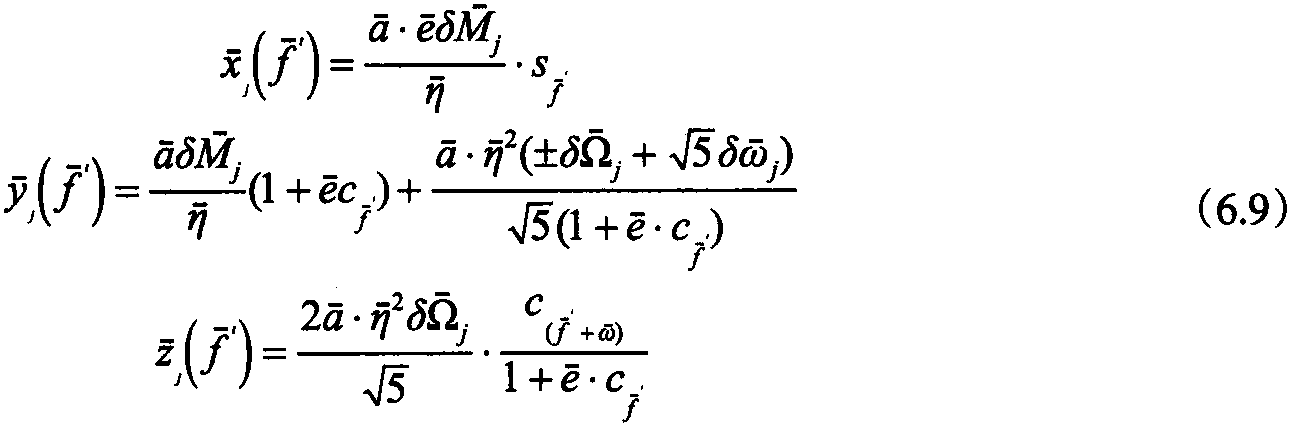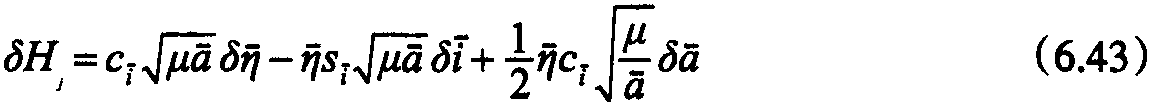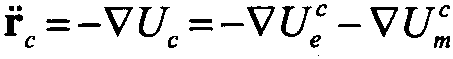
图4.1中的任意向量r在LVLH坐标系(S0-xyz)和地心坐标系(E-XYZ)表述分别为r和rE，它们的关系为
r=TrE
(4.1)
式中，T为从地心坐标系到LVLH坐标系的旋转变换，
由于参考卫星S0的角速度分量在y轴和z轴上分别为
ωy＝0
(4.3)
因此有
因为rc在(S0-xyz)坐标系中可以表示为
rc＝rc
(4.7)
对求关于时间t的一阶导数，可得
假设4.1： 地球与卫星之间的距离远小于月球与卫星之间的距离，即
rc≪qc，rd≪qd
(4.9)
根据该假设，可将地心坐标系近似地看作惯性坐标系。
假设4.2： 中心天体为匀质的理想球体，亦即其引力场为球形引力，其他非球形引力摄动不存在。
根据该假设，可以在研究中突出第三体摄动对卫星运动的影响，忽略中心天体及第 ...... （共3898字） [阅读本文]>>
长寿卫星编队飞行理论我们在以前的研究中提出了用6个参考卫星轨道要素 (RSV)来描述参考卫星的地球轨道运动。这6个轨道要素是： 卫星到地心的距离及其变化率(r，vx)，轨道倾角i，纬度幅角θ，轨道角动量h和升交点赤经Ω。
长寿卫星编队飞行理论目前，国外研究的重点在于对Hill方程或者改进的Hill方程进行细致的摄动影响分析，并取得了很好的成果; 国内张玉锟研究了编队卫星的动力学和运动学设计方法，并以此为基础进行了大量的摄动分析研究，但对于
长寿卫星编队飞行理论在上一节中，在临界倾角处利用“严格J2不变轨道”条件，卫星的自然周期类圆形卫星编队已经被设计提出，并且通过STK高精度仿真，得到了很好的效果，证明设计是非常准确的。但是由于“严格J2不变轨道”条件约束
长寿卫星编队飞行理论本章设计了一种能够顺从J2摄动的自然周期类圆形编队作为卫星编队的目标轨道，并且本课题设计的目标轨道是以约束方程表述的、且独立于终端时刻，构造了终端时刻自由的最省燃料控制问题。9.1.1 相对运动方程考
卫星编队最初是由NASA(美国国家航空航天局)和美国空军提出的，卫星编队飞行是由多颗功能类似的卫星，在空间上构成一定几何形状，总体相互协同、通信共同完成空间任务的分布式卫星系统，是未来空间技术发展的新趋
上一篇