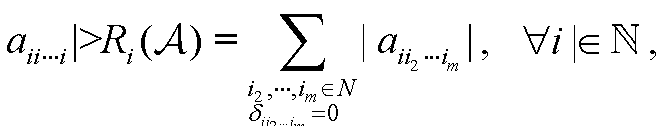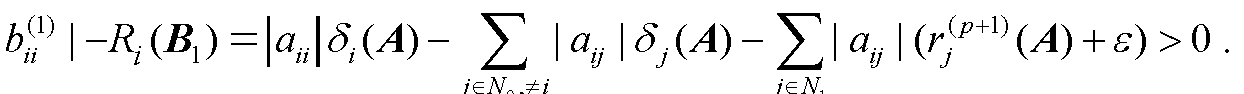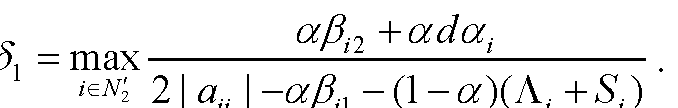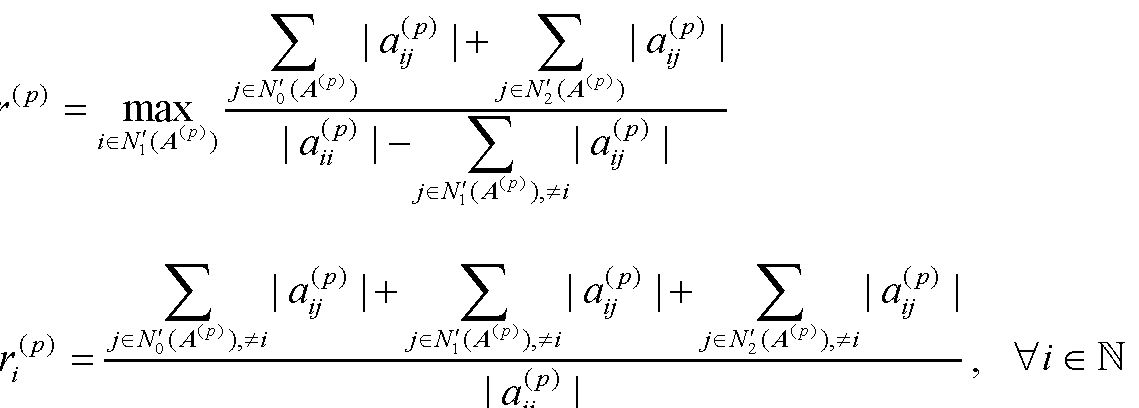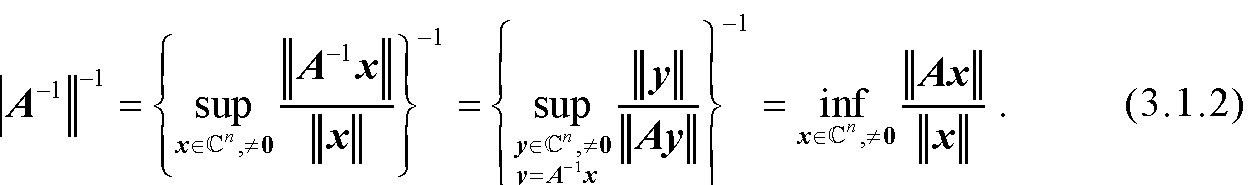
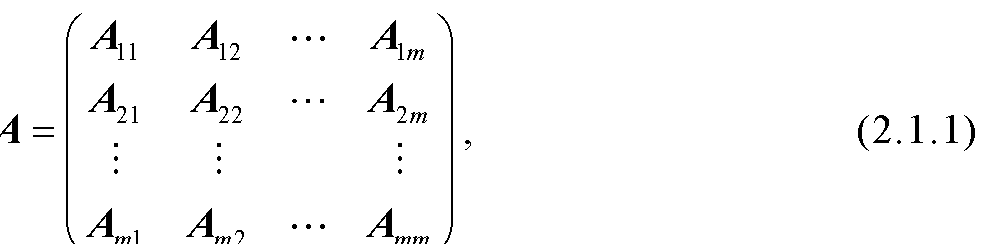
设A=(aij)∈Cn×n，如果βN，用|β|表示集合β的基数.对于非空集合β，γN，用A(β，γ)表示A中行指标位于β内、列指标位于γ内的子矩阵，其中子矩阵A(β，β)简写为A(β).设βN，=N/β，A(β)是A的非奇异子阵，称
为A关于A(β)的Schur补.设A=(aij)∈Cn×n，A的比较矩阵μ(A)=(αij)定义如下：若A能写成A=sI-B，其中B是非负矩阵，s>ρ(B)，ρ(B)为B的谱半径，则称A为M-矩阵.记Mn为所有M-矩阵所构成的集合. A∈Hn当且仅μ(A)∈Mn[80].设A=(aij)∈Cn×n，A进行如下分块 ...... （共2108字） [阅读本文]>>
H-矩阵(张量)的判定及其Schur补研究本节将介绍本书所研究问题的历史发展和意义.H-矩阵的定义是A.M.Ostrowski于1937年首先给出的[3，4]，现在H-矩阵的最直观定义是其比较矩阵为M-矩阵[5]. 实际上，M-矩阵类是H-矩
H-矩阵(张量)的判定及其Schur补研究下面介绍几类重要的特殊H-矩阵.定义2.1设矩阵A=(aij)∈Cn×n，N={1，2，…，n}，记Ri(A)=|aij|，Ci (A)=|aij|，若对任意i，j∈N，i≠j，(ⅰ)|aii|>
H-矩阵(张量)的判定及其Schur补研究本节通过递进选取对角矩阵因子元素，得到H-矩阵的一些新的判定方法，再进一步将此类判定方法推广到不可约矩阵和具有非零元素链矩阵的情形，并用实例说明这些方法的有效性.为了叙述方便，先引入下列记号： 设A=
H-矩阵(张量)的判定及其Schur补研究引进下述记号：设N1，N2N， N1∪N2=N， N1∩N2=∅， α∈(0，1]，
H-矩阵(张量)的判定及其Schur补研究H-矩阵的构造判别法就是构造一个正对角矩阵X，再把它右乘到需要判定的矩阵上，如果乘积矩阵是严格对角占优矩阵，则判别成功. 这样的判别过程从矩阵理论上来说比较简洁方便，但实际可操作性并不强，特别是对大型
上一篇