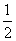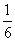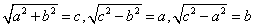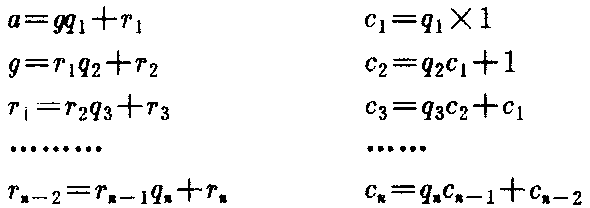
今有物，不知其数。三、三数之，剩二;五、五数之，剩三;七、七数之，剩二。问物几何?
术曰：三、三数之剩二，置一百四十;五、五数之剩三，置六十三;七、七数之剩二，置三十。并之，得二百三十三。以二百一十减之，即得。凡三、三数之剩一，则置七十;五、五数之剩一，则置二十一;七、七数之剩一，则置十五。一百六以上，以一百五减之，即得。
南北朝《孙子算经》卷下
【评】此“物不知数”问是中国数学史上第一次明确提出的一次同馀式组问题。根据题设，它是求满足同余式组N≡2(mod3)≡3(mod5)≡2(mod7)的最小正整数N。其解答为N=2×70+3×21+2×15-2×105=23，并说明了70，21，15的选择为70≡1(mod3)，21 ...... （共4063字） [阅读本文]>>
中国历代文献精粹衰分术曰：各置列衰，副并为法，以所分乘未并者各自为实，实如法而一。不满法者，以法命之。汉《九章算术·衰分》【评】这是完整的比例分配算法。列衰即是相与率。设所分为A，列衰为ai(i=1，2，…n)，则每一
中国历代文献精粹(环田)术曰：并中外周而半之，以径乘之，为积步。汉《九章算术·方田》【评】这是《九章》提出的圆环的面积公式，历代沿用：S=(l1+l2)d。其中S，l1，l2，d分别是环田面积，外周，中周及径(d=r1
中国历代文献精粹刍童、曲池、盘池、冥谷皆同术。术曰：倍上袤，下袤从之;亦倍下袤，上袤从之，各以其广乘之，并，以高若深乘之，皆六而一。其曲池者，并上中、外周而半之，以为上袤;亦并下中、外周而半之，以为下袤。汉《九章算术·
中国历代文献精粹故折矩以为勾广三，股修四，径隅五。既方之外，半其一矩，环而共盘，得成三、四、五。两矩共长二十有五，是谓积矩。汉《周髀算经》卷上若求邪至日者，以日下为勾，日高为股。勾、股各自乘，并而开方除之，得邪至日。汉
中国历代文献精粹勾、股各自乘，并之为弦实。开方除之，即弦。按：弦图，又可以勾、股相乘为朱实二，倍之为朱实四，以勾股之差自相乘为中黄实，加差实亦成弦实①。以差实减弦实，半其馀，以差为从法，开方除之，复得勾矣。加差于勾，即
上一篇