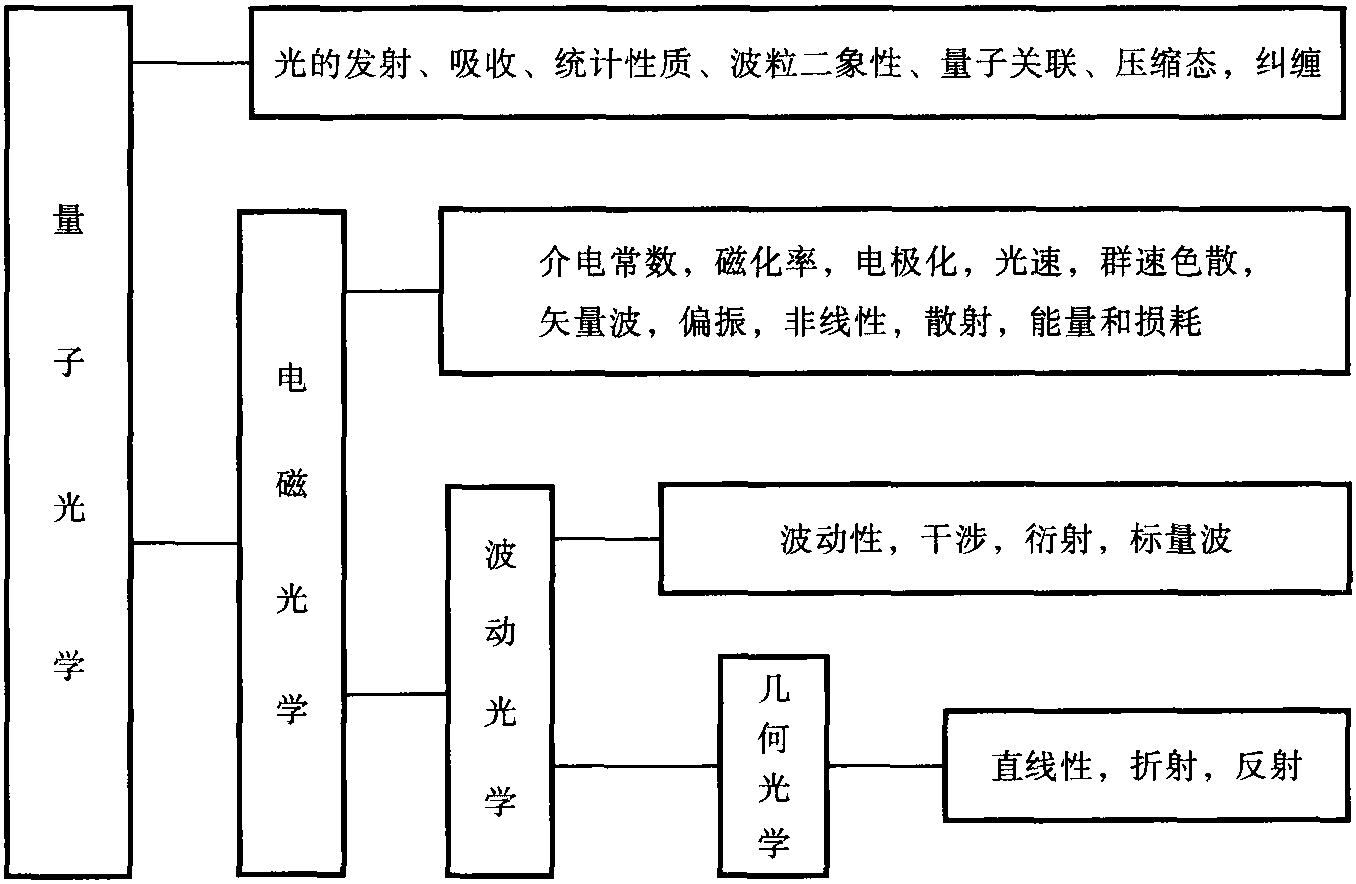
三、光线和程函方程

在忽略光的波长时,光场的性质可以用几何光学来处理。在几何光学中,光场的能量沿着一定的曲线(光线)传输,光场用光线来表征。几何光学是电磁光学的短波近似,它的所有规律都可以从麦克斯韦方程出发并取λ0→0极限得到。几何光学将有专门的一章讨论,这里仅简要阐述几何光学跟电磁光学的内在联系。
由麦克斯韦方程,各向同性非导体介质中一个一般的时谐场可以写成
E(r,t)=Re[E0(r)e-iωt] (1-79)
H(r,t)=Re[H0(r)e-iωt] (1-80)
式中,E0、H0代表位置的复数矢量函数。对于沿单位矢量s方向在折射率为n的介质中传播的均匀平面波,有E0=eeik0n(s·r),H0=heik0n(s·r) (1-81 ...... (共1332字) [阅读本文]>>
式中,e、h是常数复矢量。在远离场源很�
 上一篇
上一篇