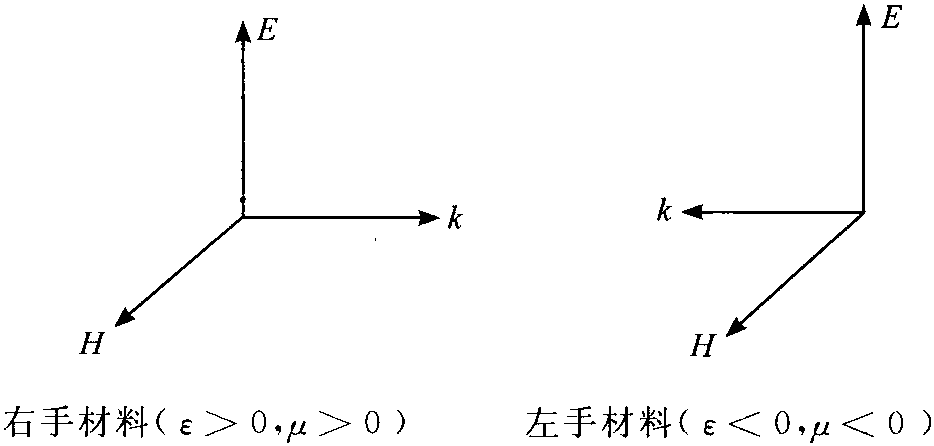
虽然到目前为止并没有在自然界中发现介电常数ε和磁导率μ都为负值的介质，但早在1968年，苏联科学家Veselago就在理论上研究了这类介质的电磁学性质[11]。事实上，麦克斯韦方程组是宏观电磁现象的普遍理论，因此介电常数ε和磁导率μ取负值时麦克斯韦方程组仍适用。各向同性介质中，考虑磁导率μ后，对于单色平面波，麦克斯韦方程组(1-30)式中的旋度方程可以写成如下形式：
k×E=ωμH (1-150)
k×H=-ωεE (1-151)
而且，只要ε和μ同号，则k2＝ω2εμ/c2>0，k取实数，平面波能在介质中传播。如图1-12所示，由(1-150)式和(1-151)式可知，对介电常数和磁导率为正的常规材料，E、H和k三者之间构成右手螺旋关系，现 ...... （共2771字） [阅读本文]>>
光学目前光学领域内遇到的绝大部分现象和技术，都能从电磁光学得到很好的解释。描述光和物质相互作用的经典理论、半经典理论，均把光辐射视为经典电磁波，遵从光的电磁理论。在整个电磁频谱中，可见光只占很小一部分。由表
光学在国际单位制的体系下，麦克斯韦方程组有最简单的形式：式中，H(r，t)是磁场强度矢量(magneticfieldvector，单位：A/m)，E(r，t)是电场强度矢量(electricfieldvec
光学磁感应强度矢量的散度等于0，这表示它本身是由矢量的旋度产生的。因为对于任意矢量都有：▽·(▽×A)=0，所以，(1-4)式表示有矢量势的存在，令B=▽×A(1-18)A(r，t)是矢量势(vectorp
光学波动方程首先研究没有场源存在的介质中电磁波的传播。在线性、非色散、均匀和各向同性的介质中，假定介质中不存在电流、空间电荷，不考虑铁磁性，也不考虑电极化的高阶项。这时，麦克斯韦方程组变成式中，介电常数和磁
光学在考虑色散、非均匀或者各向异性介质中的传输时，介电张量和磁导率都不能认为是常数，而是与位置和方向相关的函数。对于无增益、无损耗的非均匀、非铁磁介质，麦克斯韦方程组是式中第二式可写为对方程两边分别作旋量运
上一篇