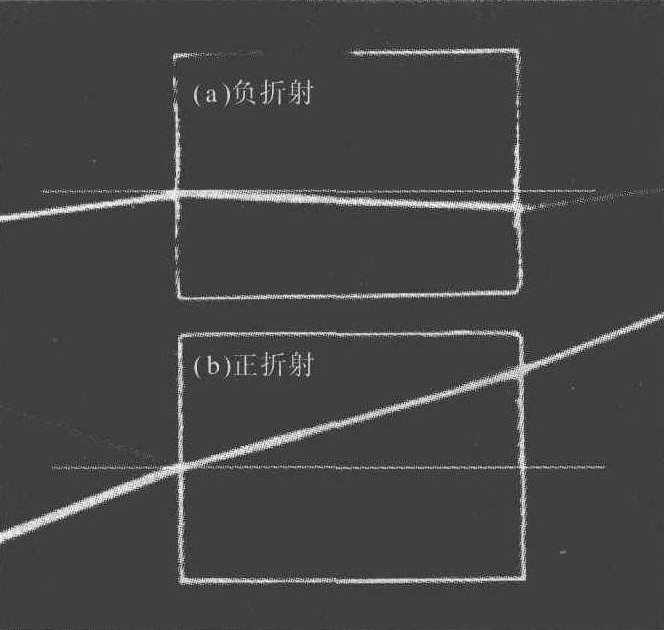
由(1-175)式，入射波矢位于法线一侧，而反射波矢、折射波矢位于法线的另一侧;而且，随着波矢入射角的逐渐减小，波矢反射角和波矢折射角也逐渐减小。当θi＝0时，θr＝θt＝0。由(1-180)式，单轴晶体内e光光线与波矢不重合。对光从各向同性介质入射到单轴晶体的情形，可以选择合适的光轴取向，对负单轴晶体使折射波矢位于光轴和界面法线之间，对正单轴晶体使折射波矢与光轴位于界面法线两侧。于是，对于较大的θt，折射光线与折射波矢位于法线同侧，但折射光线比折射波矢更靠近界面法线，光线折射角θst小于θt。随着入射角θi的不断减小，折射波矢不断靠近界面法线，折射光线将越过法线， ...... （共1219字） [阅读本文]>>
光学目前光学领域内遇到的绝大部分现象和技术，都能从电磁光学得到很好的解释。描述光和物质相互作用的经典理论、半经典理论，均把光辐射视为经典电磁波，遵从光的电磁理论。在整个电磁频谱中，可见光只占很小一部分。由表
光学在国际单位制的体系下，麦克斯韦方程组有最简单的形式：式中，H(r，t)是磁场强度矢量(magneticfieldvector，单位：A/m)，E(r，t)是电场强度矢量(electricfieldvec
光学磁感应强度矢量的散度等于0，这表示它本身是由矢量的旋度产生的。因为对于任意矢量都有：▽·(▽×A)=0，所以，(1-4)式表示有矢量势的存在，令B=▽×A(1-18)A(r，t)是矢量势(vectorp
光学波动方程首先研究没有场源存在的介质中电磁波的传播。在线性、非色散、均匀和各向同性的介质中，假定介质中不存在电流、空间电荷，不考虑铁磁性，也不考虑电极化的高阶项。这时，麦克斯韦方程组变成式中，介电常数和磁
光学在考虑色散、非均匀或者各向异性介质中的传输时，介电张量和磁导率都不能认为是常数，而是与位置和方向相关的函数。对于无增益、无损耗的非均匀、非铁磁介质，麦克斯韦方程组是式中第二式可写为对方程两边分别作旋量运
上一篇