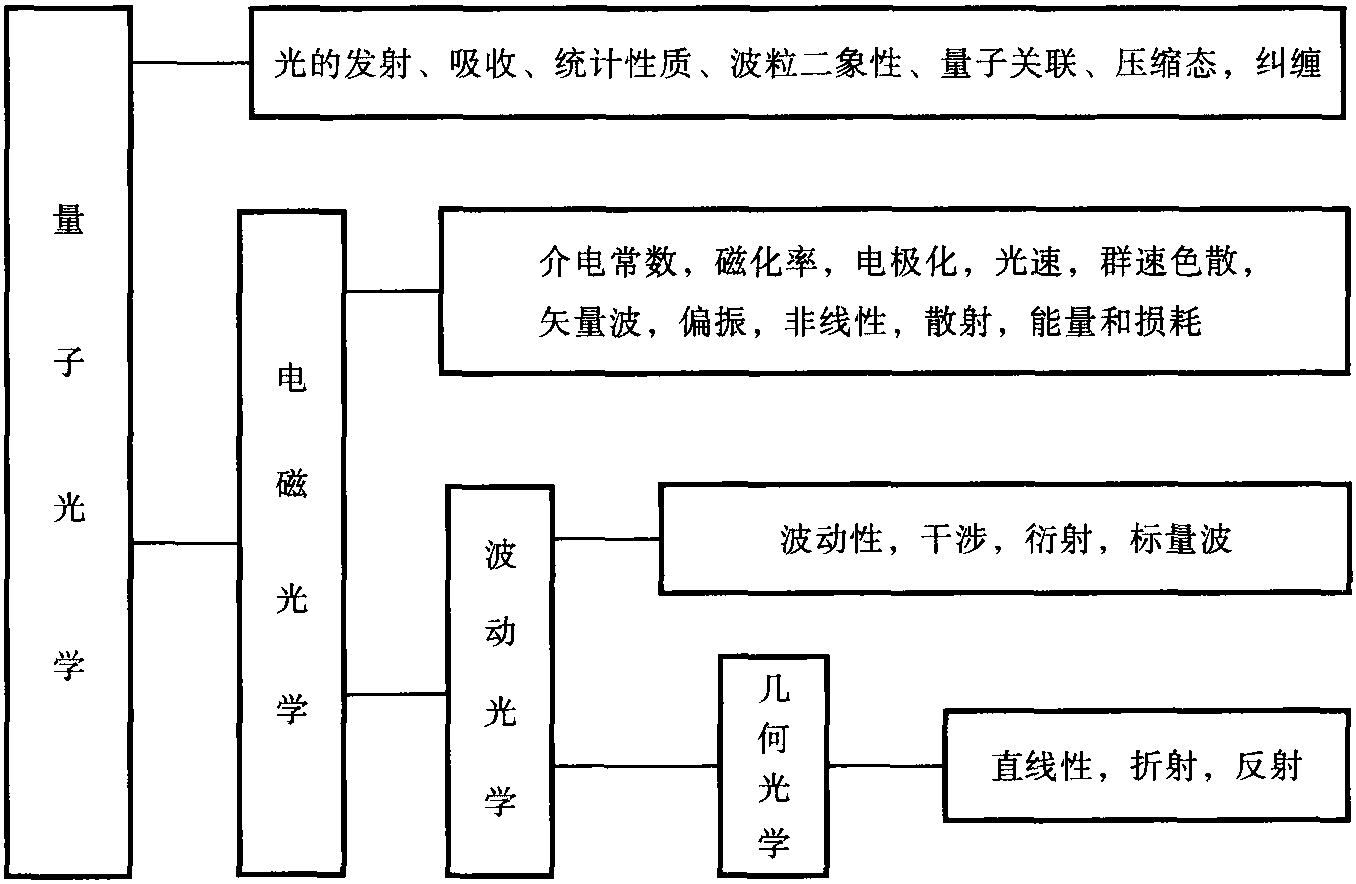
四、数值方法
电磁场方程通常只在特定的边界条件和初始条件下有解析解。对于大量的实际遇到的情况,光场的时空分布状态靠数值解。因此,数学模拟有特殊重要的意义。例如,近代很多光学实验都是首先在计算机上完成的,很多新型的光学器件也是首先在计算机上被证明的,新型光学器件的设计更是要靠计算机。大量计算机的应用研究,推动着电磁场的计算方法本身的不断发展,正在不断加深对电磁光学的认识和理解,探索和发现新的电磁光学现象。下面介绍两种常用的算法:分步傅里叶算法和有限差分法 ...... (共222字) [阅读本文]>>

 上一篇
上一篇