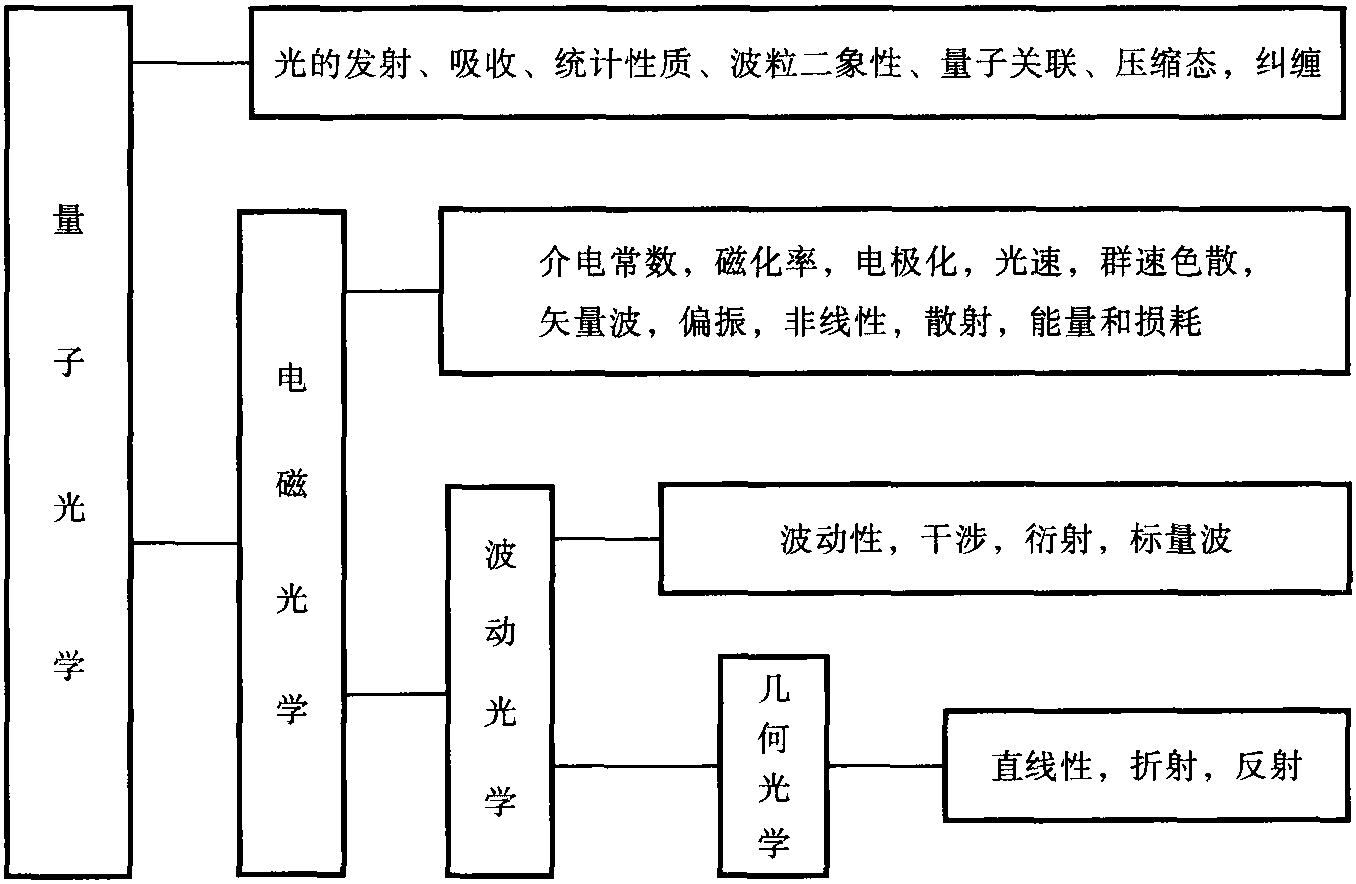
非线性薛定谔方程的推导，利用了慢变包络近似，忽略了复振幅的二阶导数，而且通常是考虑一维传输情况。根据实际情况，会考虑用有限差分法(finite-difference methods)取代分步傅里叶计算方法，直接从麦克斯韦最基本的波动方程求解。例如集成波导器件的设计与分析[67]、三维光束的传输[68]、三维形貌分析[69]、激光与物质的相互作用[70]和全息存储[71]等。这些拓展的算法克服了为求得解析解而必需的假设条件的限制，能包括光的双向传输、光的矢量性质和偏振性质、光与物质的相互作用等。新发展的算法尽可能地少使用近似条件，自然是更准确，唯一的问题是增加了计算的工作量。因此，用最少的 ...... （共414字） [阅读本文]>>
光学目前光学领域内遇到的绝大部分现象和技术，都能从电磁光学得到很好的解释。描述光和物质相互作用的经典理论、半经典理论，均把光辐射视为经典电磁波，遵从光的电磁理论。在整个电磁频谱中，可见光只占很小一部分。由表
光学在国际单位制的体系下，麦克斯韦方程组有最简单的形式：式中，H(r，t)是磁场强度矢量(magneticfieldvector，单位：A/m)，E(r，t)是电场强度矢量(electricfieldvec
光学磁感应强度矢量的散度等于0，这表示它本身是由矢量的旋度产生的。因为对于任意矢量都有：▽·(▽×A)=0，所以，(1-4)式表示有矢量势的存在，令B=▽×A(1-18)A(r，t)是矢量势(vectorp
光学波动方程首先研究没有场源存在的介质中电磁波的传播。在线性、非色散、均匀和各向同性的介质中，假定介质中不存在电流、空间电荷，不考虑铁磁性，也不考虑电极化的高阶项。这时，麦克斯韦方程组变成式中，介电常数和磁
光学在考虑色散、非均匀或者各向异性介质中的传输时，介电张量和磁导率都不能认为是常数，而是与位置和方向相关的函数。对于无增益、无损耗的非均匀、非铁磁介质，麦克斯韦方程组是式中第二式可写为对方程两边分别作旋量运
上一篇