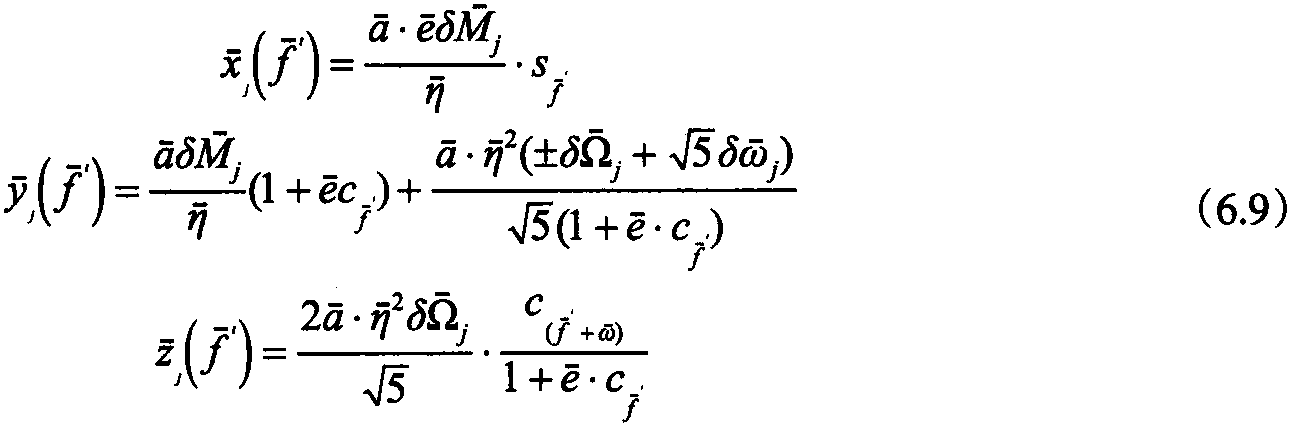7.1.1 卫星相对轨道周期运动的偏移量
有了卫星相对轨道的模型，可以从求解其偏移量入手来分析其相对运动情况，从卫星在任意一时刻在相对轨道中都存在一个具体的位置，如果经过一个周期或者多个周期后它在相对轨道的位置没有发生变化或变化甚微，说明从卫星相对主卫星的变化有较好的周期性，适用于长时间的编队作业。假设卫星运动的自然周期运动为T，在t0时刻卫星真近点角为f0，经过一个周期后，真近点角和时间分别有如下变化
f0→f0+2π⇔t0→t0+T
(7.1)
从卫星Sj经过一个周期在以主卫星S0为原点的相对坐标系的位置都有相应的变化，映射到3个坐标轴上，如下所示
如果经过一个周期，从卫星相 ...... （共2160字） [阅读本文]>>
长寿卫星编队飞行理论我们在以前的研究中提出了用6个参考卫星轨道要素 (RSV)来描述参考卫星的地球轨道运动。这6个轨道要素是： 卫星到地心的距离及其变化率(r，vx)，轨道倾角i，纬度幅角θ，轨道角动量h和升交点赤经Ω。
长寿卫星编队飞行理论图4.1中的任意向量r在LVLH坐标系(S0-xyz)和地心坐标系(E-XYZ)表述分别为r和rE，它们的关系为r=TrE (4.1)式中，T为从地心坐标系到LVLH坐标系的旋转变换，由于参考卫星S0
长寿卫星编队飞行理论目前，国外研究的重点在于对Hill方程或者改进的Hill方程进行细致的摄动影响分析，并取得了很好的成果; 国内张玉锟研究了编队卫星的动力学和运动学设计方法，并以此为基础进行了大量的摄动分析研究，但对于
长寿卫星编队飞行理论在上一节中，在临界倾角处利用“严格J2不变轨道”条件，卫星的自然周期类圆形卫星编队已经被设计提出，并且通过STK高精度仿真，得到了很好的效果，证明设计是非常准确的。但是由于“严格J2不变轨道”条件约束
长寿卫星编队飞行理论本章设计了一种能够顺从J2摄动的自然周期类圆形编队作为卫星编队的目标轨道，并且本课题设计的目标轨道是以约束方程表述的、且独立于终端时刻，构造了终端时刻自由的最省燃料控制问题。9.1.1 相对运动方程考
上一篇