1.1.2 光学薄膜的吸收
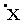
1) 共振吸收
如果把原子分子体系看做是谐振子体系,这个体系在电场E=E0e-iω t的作用下,满足强迫振动方程:
m0+m0γ+Kx=-eE0e-iω t
(1-1-21)
式中,m0为电子质量,e为电子的电荷,γ为阻尼系数,它是与原子结构及材料体系结构有关的常数,K是弹性系数。令ω20=, ω0为体系的固有角频率。则有
m0+m0γ+m0ω20x=-eE0e-iω t
(1-1-22)
解得
x=E0
(1-1-23)
总的极化强度矢量:
P=Np=-Nex=E0
(1-1-24)
电位移矢量:D=ε0εE=ε0E+P。
考虑到材料体系中原子的本征散射对介电常数的贡献,电位移矢量为
D=ε0E+ε0χE+P
ε=1+χ+
(1-1-25)
式中,χ主要取决于材料原子本身的结构参数,对应介电常数的背景项。由ε=ε1+iε2,可以得到
ε1=1+χ+
(1-1-26)
ε2=
(1-1-27)
又N=n-ik ...... (共2791字) [阅读本文]>>

 上一篇
上一篇

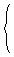
.jpg)
.jpg)