1.1.4 光学薄膜的散射
.jpg)
1.1.4.1 表面统计参量
光学材料表面微粗糙的存在,是材料本身及加工过程带来的必然结果。设z(x)是真实表面x处偏离平均平面的高度函数,由于它的高低起伏被认为是一个静态随机过程,为了更好地了解表面的特征,人们通常用数学上常用的统计参数来表征微粗糙表面的横向和纵向分布特征,如粗糙度的均方根值,表面的高度分布函数,表面的自协方差函数及表面的功率谱密度等[6]。
1) 均方根粗糙度(Root Mean Square roughness, RMS)
光学表面的粗糙度通常用表面高度起伏的均方根(RMS)值δ来表示。理想情况下,它的严格数学定义为
δ2L=∫L-Lz2(x)dx=〈∫L-Lz2(x)dx〉
(1-1-67)
式中,z(x)为x点处的表面高度值,〈·〉表 ...... (共13514字) [阅读本文]>>

 上一篇
上一篇

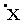
.jpg)