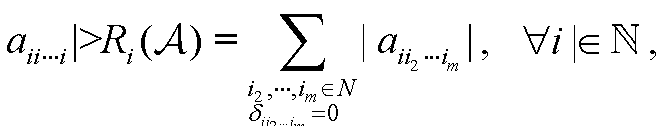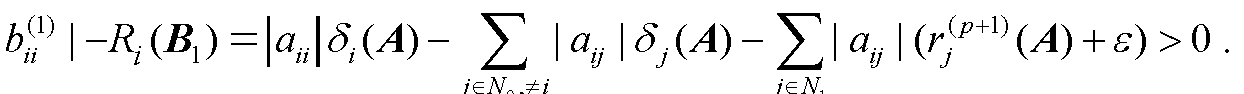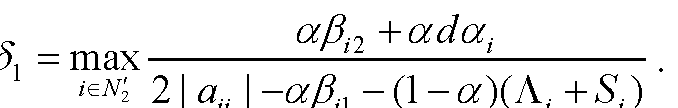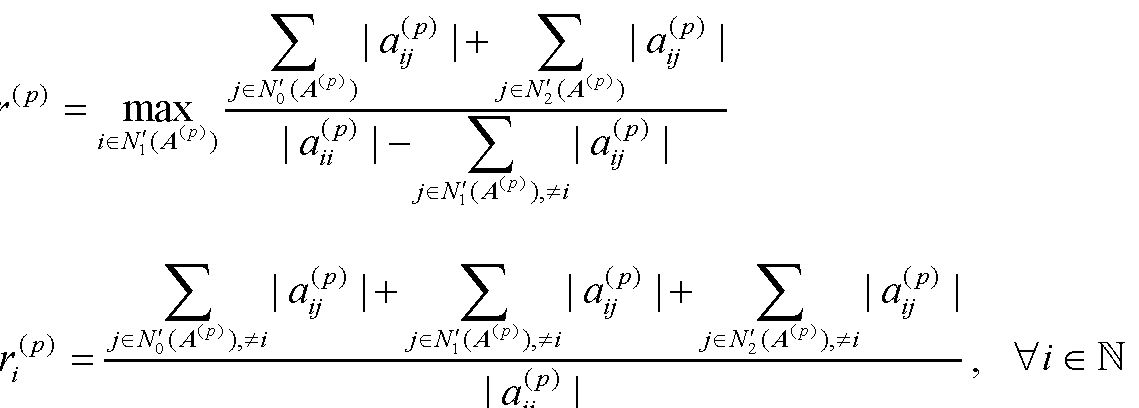您现在的位置是：首页 > 科普 > H-矩阵(张量)的判定及其Schur补研究

4.1 H-张量的性质

分类：H-矩阵(张量)的判定及其Schur补研究2441字

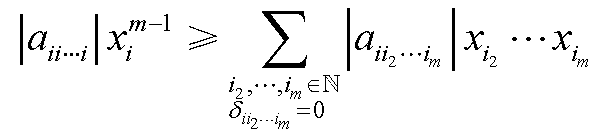
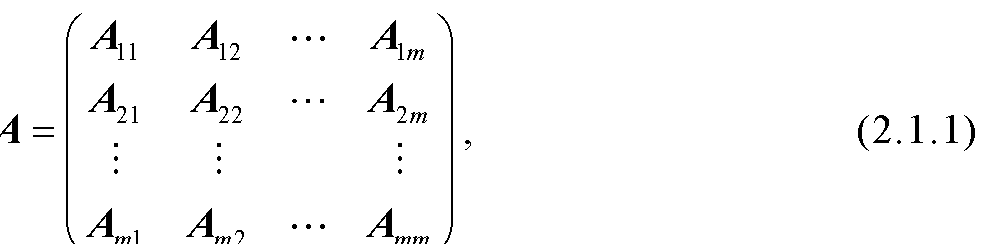
为方便讨论，先给出如下符号：设A=[ai1i2…im]∈C[m，n]，记

下面给出张量的几个性质.性质4.1 设A=[ai1i2…im]∈C[m，n]，且akk…k≥0(k∈N)，若A是对角占优张量，则A的所有实特征值是非负的.证明 设λ为A的任一实特征值.假设λ<0，则对任意的i∈N，

但由文献[12]的定理4.1可知存在i∈N，使得

这与式 (4.1.1) 矛盾.性质得证.性质4.2 设A=[ai1i2…im]∈C[m，n]，且akk…k≥0(k∈N)，若A是严格对角占优张量，则A的所有实特征值是正的.证明 由性质4.1可直接得出结论.性质4.3 设A=[ai1i2…im]∈C[m，n]∈C是广义H-张量，则|N1(A)∪N2(A)|≥1，即至少存在一个i0∈N，使 ......     （共2441字）    [阅读本文]>>

证明 因为A是广义H-张量，所以存在正向量x=(x1，…，xn)T，使得对任意
其他相关分类

推荐内容