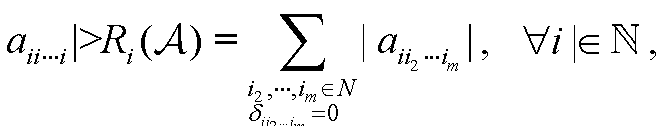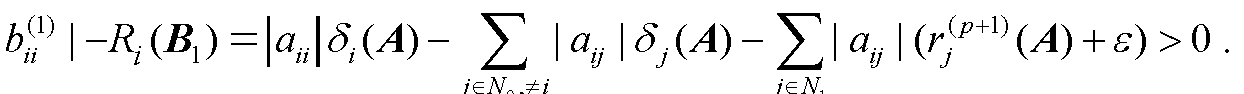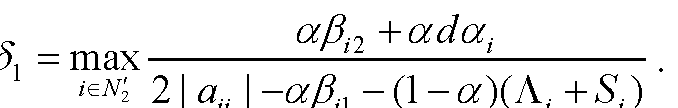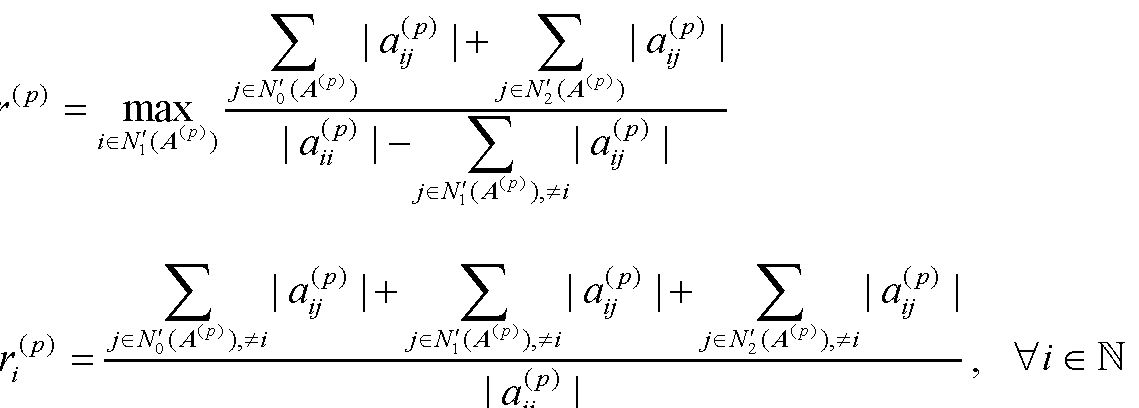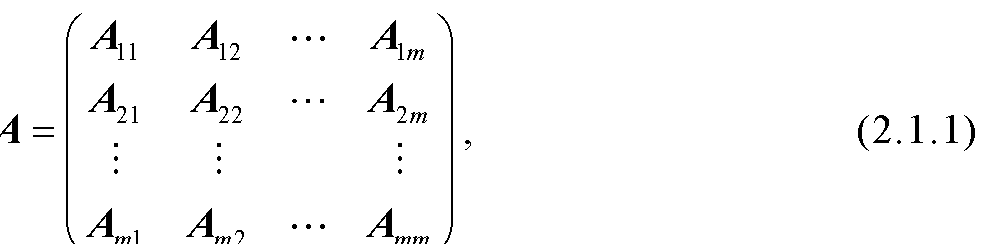
H-矩阵在计算数学、系统工程、控制理论、经济数学等领域中具有广泛的实际应用，因此判定一个矩阵是否为H-矩阵，以及研究H-矩阵类的应用是非常重要的工作.本书所得结果总结如下：(1)研究了H-矩阵的判定问题，给出了判定H-矩阵的一些充分条件和迭代判定算法，从而扩充了H-矩阵的判定条件.(2)给出了一般矩阵及其Schur补的对角占优度、α-对角占优度及特征值分布区域.(3)给出了H-矩阵的子类——Ostrowski矩阵及其Schur补的对角占优度及特征值分布区域. 作为应用，给出了Ostrowski矩阵Schur补的逆矩阵无穷大范数新上界.(4)给出了块H-矩阵的子类——Ⅰ(Ⅱ)-型块严格(双)对角占优矩阵及其Schur补的对角占优度 ...... （共585字） [阅读本文]>>
H-矩阵(张量)的判定及其Schur补研究本节将介绍本书所研究问题的历史发展和意义.H-矩阵的定义是A.M.Ostrowski于1937年首先给出的[3，4]，现在H-矩阵的最直观定义是其比较矩阵为M-矩阵[5]. 实际上，M-矩阵类是H-矩
H-矩阵(张量)的判定及其Schur补研究下面介绍几类重要的特殊H-矩阵.定义2.1设矩阵A=(aij)∈Cn×n，N={1，2，…，n}，记Ri(A)=|aij|，Ci (A)=|aij|，若对任意i，j∈N，i≠j，(ⅰ)|aii|>
H-矩阵(张量)的判定及其Schur补研究本节通过递进选取对角矩阵因子元素，得到H-矩阵的一些新的判定方法，再进一步将此类判定方法推广到不可约矩阵和具有非零元素链矩阵的情形，并用实例说明这些方法的有效性.为了叙述方便，先引入下列记号： 设A=
H-矩阵(张量)的判定及其Schur补研究引进下述记号：设N1，N2N， N1∪N2=N， N1∩N2=∅， α∈(0，1]，
H-矩阵(张量)的判定及其Schur补研究H-矩阵的构造判别法就是构造一个正对角矩阵X，再把它右乘到需要判定的矩阵上，如果乘积矩阵是严格对角占优矩阵，则判别成功. 这样的判别过程从矩阵理论上来说比较简洁方便，但实际可操作性并不强，特别是对大型
上一篇