2.2.2.2 模型参数的识别
分类:高耸烟囱结构抗风设计与风振控制199字
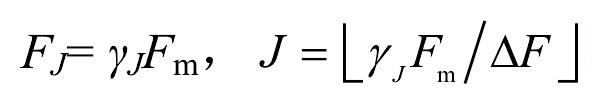
自功率谱参数 Sm、Fm、κ 可根据 S-F曲线,由式(2-49)至式(2-51)获得。
式中,为离散的无量纲频率,Nfft为傅里叶变换长度,为奈奎斯特(Nyquist)频率,,γJ 为大于 1 的松弛因子,本文取 1.5。
值得说明的是,三个自谱模型参数可以作为描述脉动风荷载频域特性的特征参数存入风荷载数据库中,便于后续应用和分析 ...... (共199字) [阅读本文]>>
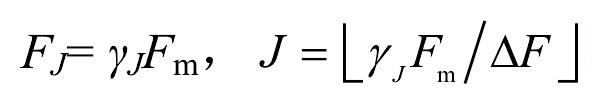
自功率谱参数 Sm、Fm、κ 可根据 S-F曲线,由式(2-49)至式(2-51)获得。
式中,为离散的无量纲频率,Nfft为傅里叶变换长度,为奈奎斯特(Nyquist)频率,,γJ 为大于 1 的松弛因子,本文取 1.5。
值得说明的是,三个自谱模型参数可以作为描述脉动风荷载频域特性的特征参数存入风荷载数据库中,便于后续应用和分析 ...... (共199字) [阅读本文]>>
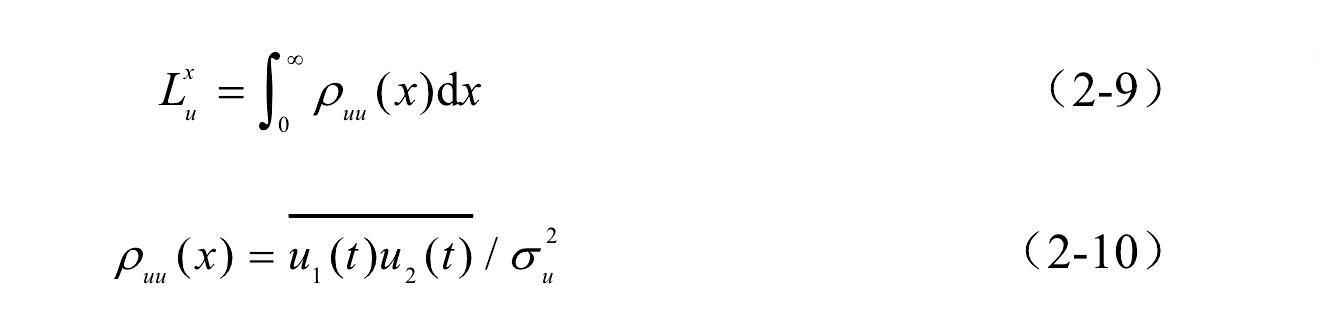 高耸烟囱结构抗风设计与风振控制
高耸烟囱结构抗风设计与风振控制由于风的随机性,脉动风速三分量 u(t),v(t),w(t)均为随机过程,一般可假定成均值为零的平稳随机过程,其均方根值分别为 σu,σv,σw。分别采用顺风向、横风向和竖向的湍流强度(Turbule
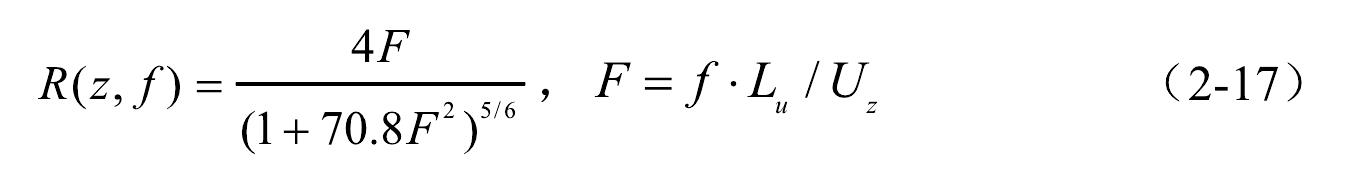 高耸烟囱结构抗风设计与风振控制
高耸烟囱结构抗风设计与风振控制大气边界层的自然风为湍流风,在微观气象尺度范围内,由于气流的不稳定性,其随机周期的变化范围从零点几秒到几分钟不等。对于高度 z(m)处的顺风向湍流风速 u(z,t)(m/s),其频率的概率分布可通过无
 高耸烟囱结构抗风设计与风振控制
高耸烟囱结构抗风设计与风振控制20 世纪 60 年代,Davenport [119]基于结构附近未扰动风的湍流特征提出了位于大气边界层内结构的脉动风荷载模型,对于微面或点状结构,基于拟定常假设式中,Cp为风压系数;该假设将来流全脉
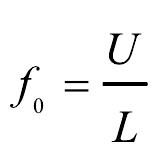 高耸烟囱结构抗风设计与风振控制
高耸烟囱结构抗风设计与风振控制借鉴风速谱模型式(2-20),将无量纲谱表达为如下形式:式中,为无量纲风荷载谱, Sp(f) 为单边风荷载谱(N2·s), f 为频率(Hz),为脉动风荷载总能量(方差 N2),为无量纲频率,f0
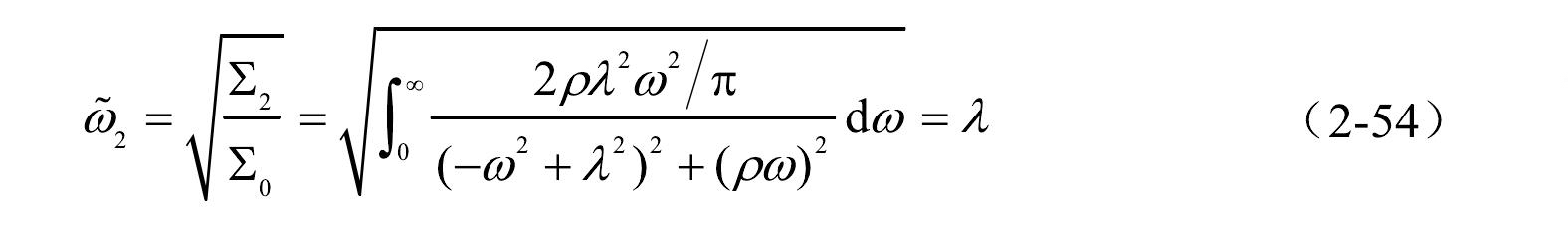 高耸烟囱结构抗风设计与风振控制
高耸烟囱结构抗风设计与风振控制根据附录 B介绍,滤波模型通常是有理函数的形式,有时分子也可以为分数阶的幂函数。因此,需确定分子与分母多项式的阶数,假设归一化的风压自功率谱表达为如下形式,式中,滤波多项式假设为二次多项式,其中,ρ、