6.2 线性自由振动系统
6.2.1 单自由度线性振动系统
单自由度线性系统自由振动的动力学方程为:
mx+rx+kx=0
(1.1.1-49)
通过一个独立坐标即可确定振动过程中任一瞬时的位置,而且r为x的线性函数,k为x的线性函数,因而微分方程是线性的,所以称为线性振动系统。上述方程所确定的运动,与系统的阻尼大小有关。在小阻尼情况下,线性微分方程的通解为:
x=Ae-atsin(ωrt+)
(1.1.1-50)
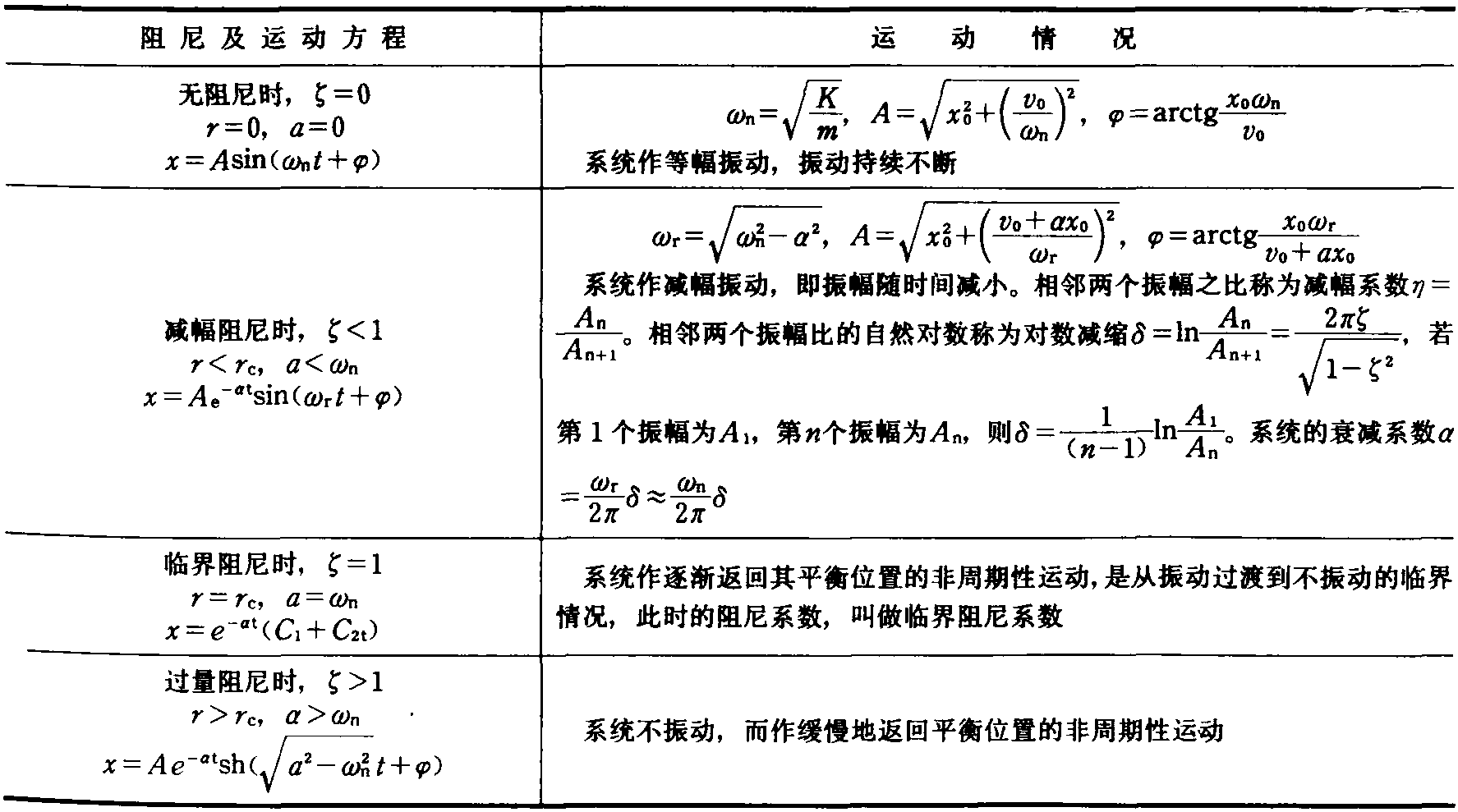
其运动情况与阻尼的大小及初始干扰有关。表1.1.1-25给出有初始位移x=x0,初速度dx/dt=x=V0时运动方程中的各项计算结果。表1.1.1-25 单自由度系统自由振动的运动情 ...... (共1874字) [阅读本文]>>
表中: m——振动体的质量; K——弹簧的刚度; r——阻尼系数; rc——临界阻尼系数rc=2; �
 上一篇
上一篇