1.3 二向应力状态的分析
分类:机械工程材料测试111字
二向应力状态要解决的问题是,已知过一点任意两个正交截面上的应力分量:σx,σy和τxy=τyx,如何求得过该点与x轴正向成任意角α的斜截面上的应力、该点的主平面、主应力、最大剪应力及其作用面等。解决的办法有解析法和图解法 ...... (共111字) [阅读本文]>>
二向应力状态要解决的问题是,已知过一点任意两个正交截面上的应力分量:σx,σy和τxy=τyx,如何求得过该点与x轴正向成任意角α的斜截面上的应力、该点的主平面、主应力、最大剪应力及其作用面等。解决的办法有解析法和图解法 ...... (共111字) [阅读本文]>>
 机械工程材料测试
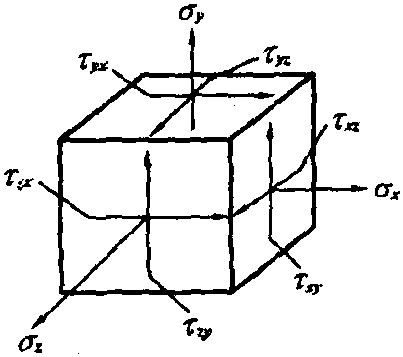
机械工程材料测试为了研究物体内某一点的应力状态,取一个很小(包含这一点在内)的六面体(又称单元体),使六面体的面分别与直角坐标的x,y和z轴垂直,见图2-1-1。图2-1-1直角坐标系中单元体上的应力分量一点的应力状态
 机械工程材料测试
机械工程材料测试由于物体的几何形状、受力状态和边界(支承)条件的不同,其应力状态也不尽相同,为了研究和计算方便必须将它分类。为此,首先定义二个概念;主平面——剪应力为零的平面称为主平面。任何一个单元体通过旋转都可找到对
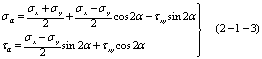 机械工程材料测试
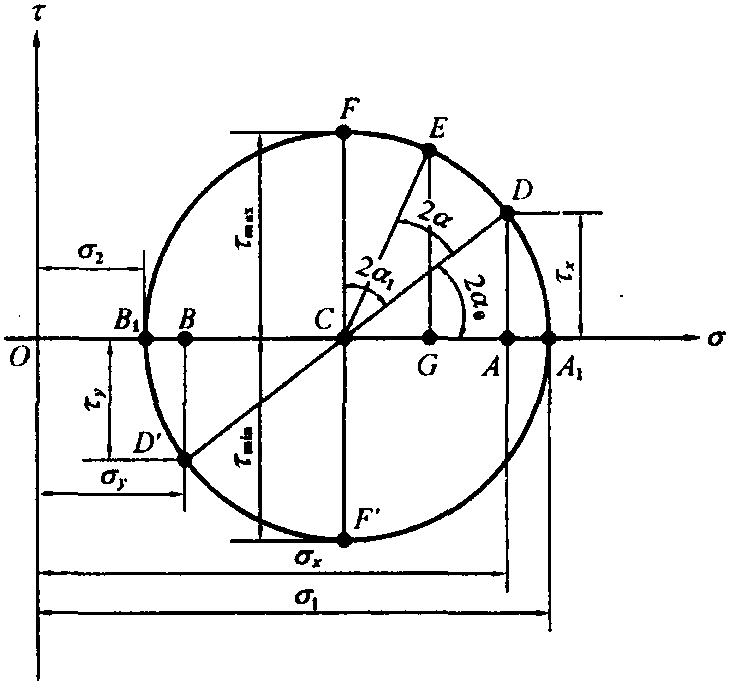
机械工程材料测试a.任意斜截面上的应力式中σα,τα为任意斜截面上的正应力和剪应力(MPa)。b.主应力c.主平面α0的两个值(即α0和α0+π/2)分别对应于两个主平面,其主应力分别为σ1和σ2。d.最大剪应力及其作
 机械工程材料测试
机械工程材料测试1.莫尔圆的画法图解法又称莫尔圆法或应力圆法,其作法见图2-1-2,取横坐标为正应力σ,纵坐标为剪应力τ,截取OA=σx,OB=σy,然后过A点作σ轴的垂线段AD=τxy,同样,过B点作σ轴的垂线段BD
 机械工程材料测试
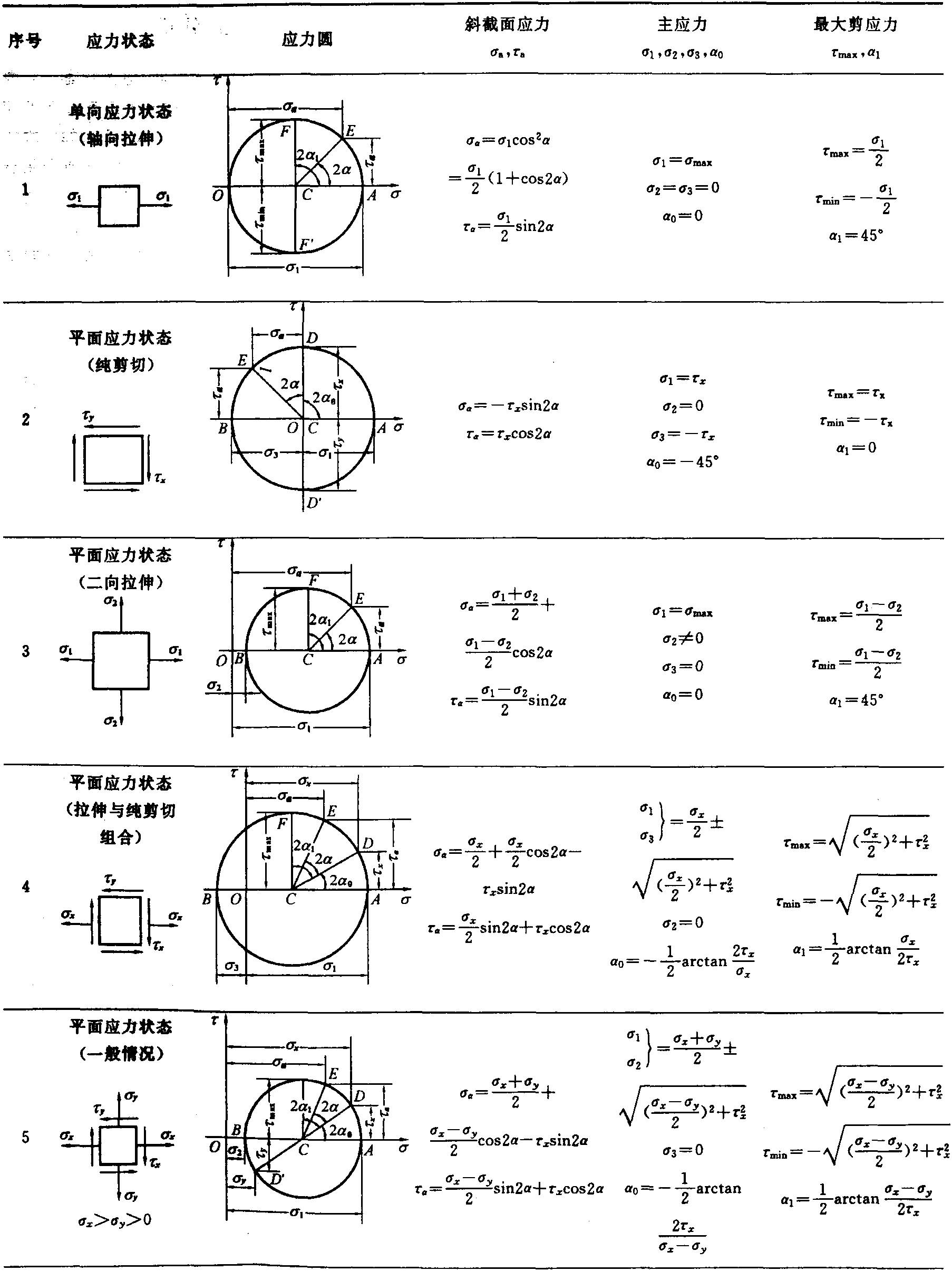
机械工程材料测试在工程实践中,大部分零部件都可近似地简化为受单向应力状态或平面应力状态,从而得到一个初步的应力估计值。当然,严格地说,三向应力状态是最普遍的,当要求较高时,可用有限元法加以计算。例如:受压的柱体、受弯曲