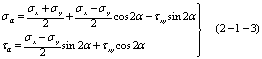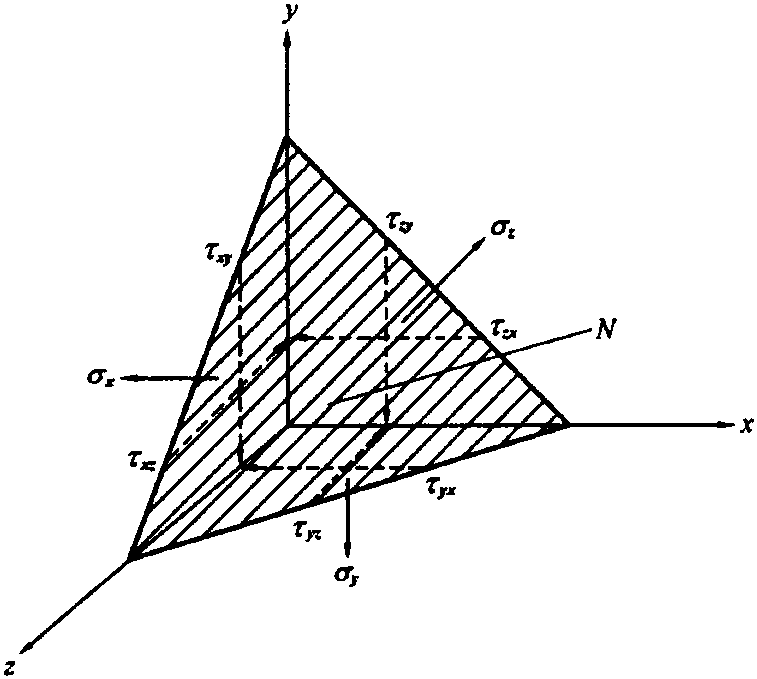
a. 任意斜截面上的应力 见图2-1-4，任意斜截面的外法线N与x，y和z轴的夹角的余弦分别为l，
图2-1-4 外法线为N的任意斜截面
m和n，则此截面上的应力表达式为正应力
σN＝σxl2+σym2+σzn2+2lmτxy+2mnτyz+2nlτxz(2-1-8)
剪应力
全应力
全应力 pN在x，y，z轴上的分量：
pNx＝σxl+τyxm+τzxn
pNy＝τxyl+σym+τxyn
pNz＝τxzl+τyzm+σzn
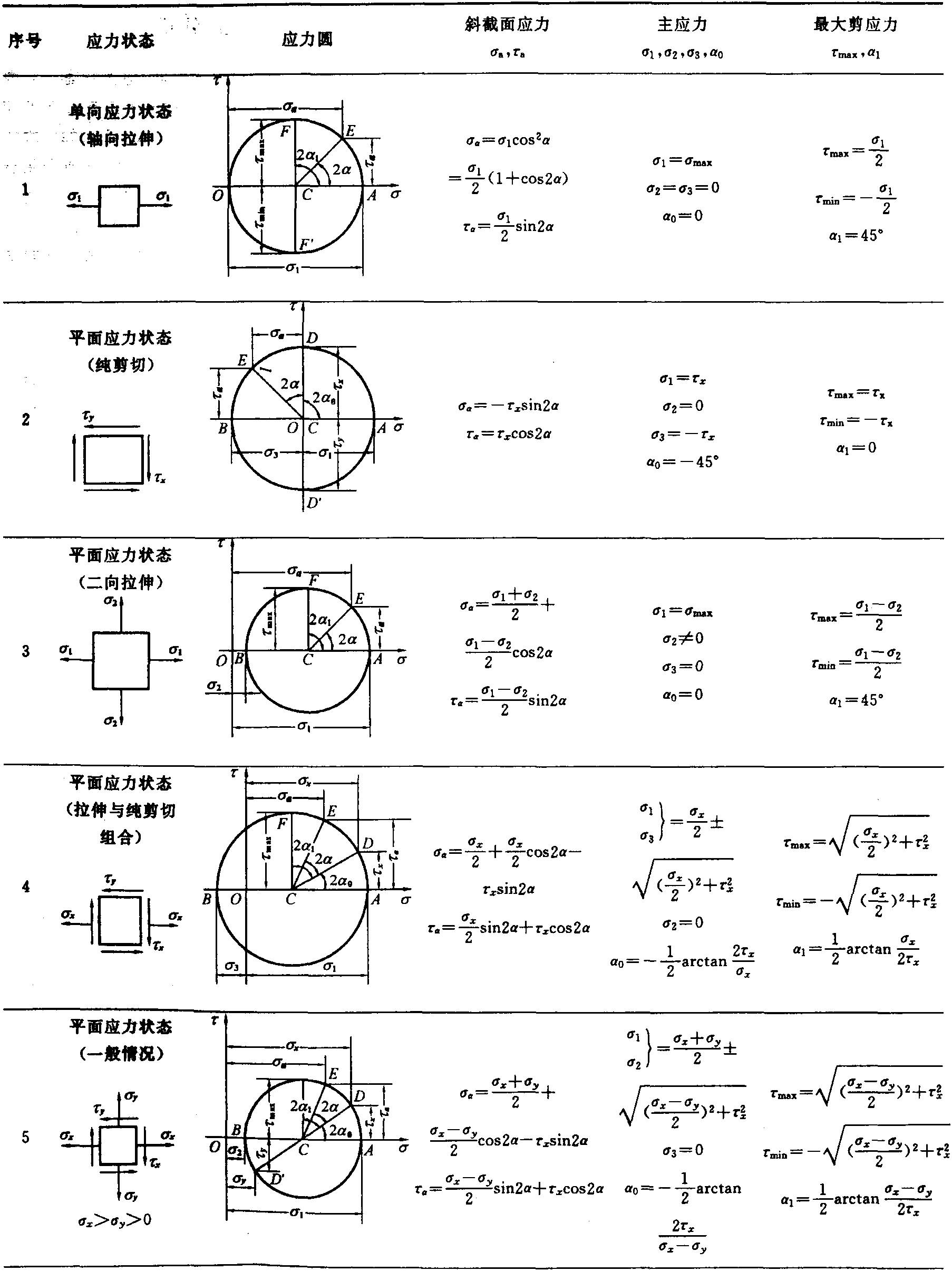
b. 主应力和主平面 该点的主应力σ1，σ2和σ3是式(2-1-11)的三个根。
σ2-σⅠ·σ2+σⅡ·σ-σⅢ＝0 (2-1-11)
式中σⅠ，σⅡ和σⅢ分别为应力状态的第一，第二和第三应力不变量。分别为
上述σⅠ，σⅡ和σⅢ均不随坐标的变换而变化，所以称为应力不变量。
对应于主应力σ1，σ2和σ3的三个主平面的外法线的方向余弦， ...... （共1476字） [阅读本文]>>
机械工程材料测试为了研究物体内某一点的应力状态，取一个很小(包含这一点在内)的六面体(又称单元体)，使六面体的面分别与直角坐标的x，y和z轴垂直，见图2-1-1。图2-1-1直角坐标系中单元体上的应力分量一点的应力状态
机械工程材料测试由于物体的几何形状、受力状态和边界(支承)条件的不同，其应力状态也不尽相同，为了研究和计算方便必须将它分类。为此，首先定义二个概念;主平面——剪应力为零的平面称为主平面。任何一个单元体通过旋转都可找到对
机械工程材料测试a.任意斜截面上的应力式中σα，τα为任意斜截面上的正应力和剪应力(MPa)。b.主应力c.主平面α0的两个值(即α0和α0+π/2)分别对应于两个主平面，其主应力分别为σ1和σ2。d.最大剪应力及其作
机械工程材料测试1.莫尔圆的画法图解法又称莫尔圆法或应力圆法，其作法见图2-1-2，取横坐标为正应力σ，纵坐标为剪应力τ，截取OA=σx，OB=σy，然后过A点作σ轴的垂线段AD=τxy，同样，过B点作σ轴的垂线段BD
机械工程材料测试在工程实践中，大部分零部件都可近似地简化为受单向应力状态或平面应力状态，从而得到一个初步的应力估计值。当然，严格地说，三向应力状态是最普遍的，当要求较高时，可用有限元法加以计算。例如：受压的柱体、受弯曲
上一篇