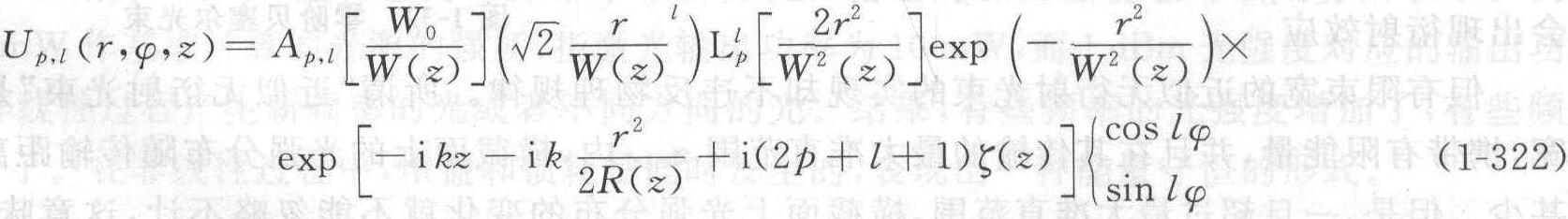
除了厄米-高斯光束是傍轴亥姆霍兹方程的一组完全解之外，在柱坐标系统(r，，z)中求解傍轴亥姆霍兹方程，还可以得到另外一组完全解，那就是拉盖尔-高斯光束(Laquerre-Gauussian beam)。最低阶拉盖尔-高斯光束也就是高斯光束。
拉盖尔-高斯光束的复振幅为[54]
式中，表示既可以取cos lp也可以取sin lp，为关联拉盖尔多项式：拉盖尔-高斯光束的强度分布是还有第三组旁轴光束的完全解，是在椭圆柱坐标中得到的，称为茵色-高斯光束(Ince-Gaussian beam)，可以方便地研究从矩形柱坐标(厄米-高斯)到对称圆柱坐标(拉盖尔-高斯)之间的横模演化。
图1-31是几个低阶拉盖尔-高斯光束的光强分布图[55]，其中01*模表示 ...... （共375字） [阅读本文]>>
光学目前光学领域内遇到的绝大部分现象和技术，都能从电磁光学得到很好的解释。描述光和物质相互作用的经典理论、半经典理论，均把光辐射视为经典电磁波，遵从光的电磁理论。在整个电磁频谱中，可见光只占很小一部分。由表
光学在国际单位制的体系下，麦克斯韦方程组有最简单的形式：式中，H(r，t)是磁场强度矢量(magneticfieldvector，单位：A/m)，E(r，t)是电场强度矢量(electricfieldvec
光学磁感应强度矢量的散度等于0，这表示它本身是由矢量的旋度产生的。因为对于任意矢量都有：▽·(▽×A)=0，所以，(1-4)式表示有矢量势的存在，令B=▽×A(1-18)A(r，t)是矢量势(vectorp
光学波动方程首先研究没有场源存在的介质中电磁波的传播。在线性、非色散、均匀和各向同性的介质中，假定介质中不存在电流、空间电荷，不考虑铁磁性，也不考虑电极化的高阶项。这时，麦克斯韦方程组变成式中，介电常数和磁
光学在考虑色散、非均匀或者各向异性介质中的传输时，介电张量和磁导率都不能认为是常数，而是与位置和方向相关的函数。对于无增益、无损耗的非均匀、非铁磁介质，麦克斯韦方程组是式中第二式可写为对方程两边分别作旋量运
上一篇