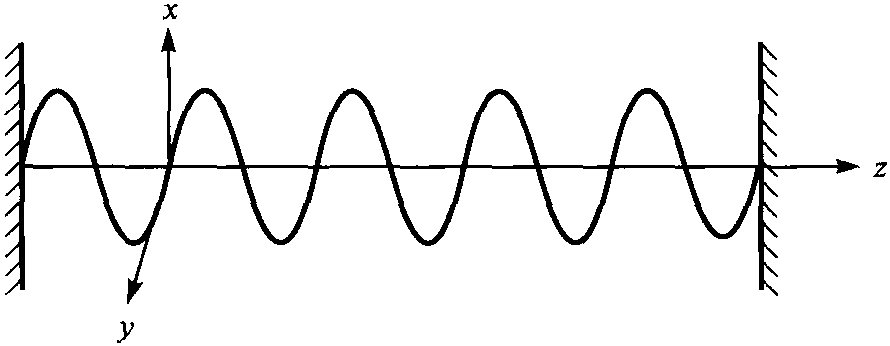
首先考虑一维谐振腔中的电磁场，如图2-1所示。设腔轴沿z方向，腔长为L。
图2-1 一维谐振腔中的电磁场
设电场沿x方向偏振，即E(r，t)=exEx(z，t)，这里ex为x方向的单位矢量。将Ex(z，t)用正则模(驻波)展开为
式中，kj＝jπ/L(由Ex(L，t)=0定出)为第j个场模的波数，qj(t)具有长度的量纲，Aj为待定常数。由麦克斯韦方程组可知，对现在考虑的情况，磁场沿y方向，即B(r，t)=eyBy(z，t)，且有式中，c=1/为真空中的光速，ωj＝ckj为第j个场模的角频率，pj(t)/mj＝dqj(t)/dt，mj具有质量的量纲，pj(t)具有动量的量纲。电磁场的总能量为式中，V是腔的体积。可见，如果令Vε0Aj2/2mjωj2＝1，即Aj＝，则 ...... （共835字） [阅读本文]>>式中，Hj为第j个场模的能量。
光学目前光学领域内遇到的绝大部分现象和技术，都能从电磁光学得到很好的解释。描述光和物质相互作用的经典理论、半经典理论，均把光辐射视为经典电磁波，遵从光的电磁理论。在整个电磁频谱中，可见光只占很小一部分。由表
光学在国际单位制的体系下，麦克斯韦方程组有最简单的形式：式中，H(r，t)是磁场强度矢量(magneticfieldvector，单位：A/m)，E(r，t)是电场强度矢量(electricfieldvec
光学磁感应强度矢量的散度等于0，这表示它本身是由矢量的旋度产生的。因为对于任意矢量都有：▽·(▽×A)=0，所以，(1-4)式表示有矢量势的存在，令B=▽×A(1-18)A(r，t)是矢量势(vectorp
光学波动方程首先研究没有场源存在的介质中电磁波的传播。在线性、非色散、均匀和各向同性的介质中，假定介质中不存在电流、空间电荷，不考虑铁磁性，也不考虑电极化的高阶项。这时，麦克斯韦方程组变成式中，介电常数和磁
光学在考虑色散、非均匀或者各向异性介质中的传输时，介电张量和磁导率都不能认为是常数，而是与位置和方向相关的函数。对于无增益、无损耗的非均匀、非铁磁介质，麦克斯韦方程组是式中第二式可写为对方程两边分别作旋量运
上一篇