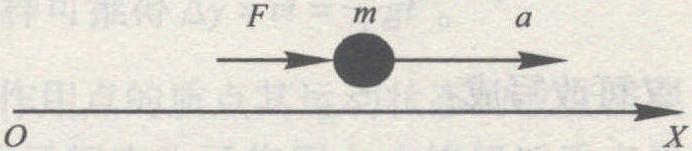
二、力的时间效应
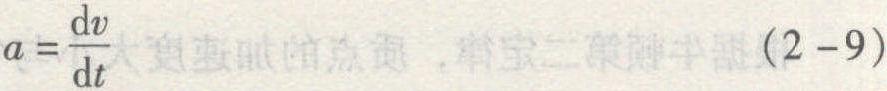
力F在t1到t2的时间间隔内的累积效应称为力F在此时间间隔内的冲量S,表示为:
S= Fdt
(2-7)
式中 Fdt——元冲量,N·S。
冲量S将引起物体动量的改变,关系式为:
S=△ (mv)=mv2-mv1
(2-8)
又加速度表达式为:
将式 (2-9) 代入式 (2-1),且视m为常量,则可得到更普遍的公式:
又可改写成:
d (mv)=Fdt (2-11)
对上式在t1到t2间隔内积分,便得到式(2-8)。
若F与v1与v2方向一致,则式 (2-8) 可写成:
mv2-mv1=Fdt
(2-12)
由式(2-9),或由式 (2-12) 可得:
△v=v2-v1= adt
(2-13)
式 (2-13) 说明速度的改变量等于加速度曲线在t1到t2间所包围的面积 (图2-2),其大小与加速度曲线 (波形、峰值)、时间间隔有关。显然这个面积的大小也表征了物体动量的改变量
...... (共1466字) [阅读本文]>>
 上一篇
上一篇