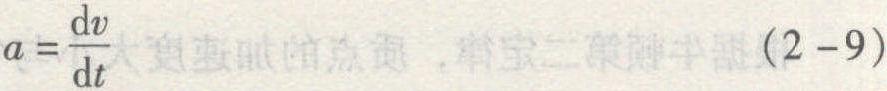1. 功
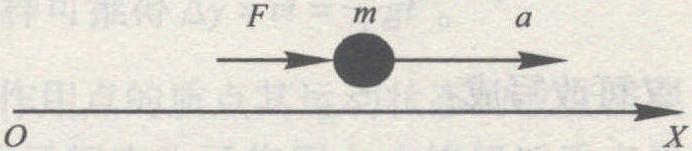
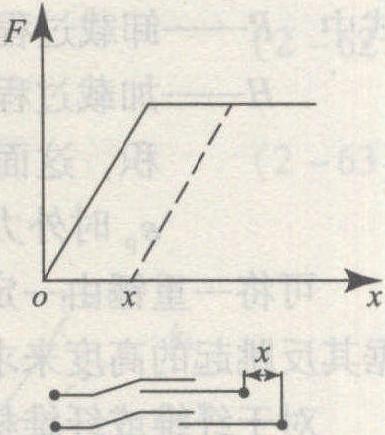
力F在位移dr上的效应被定义为力F的元功：
δW=F·dr (2-14)
这里使用变分符号δ，是因为F·dr不一定是全微分。
由于dr=vdt，则式 (2-14) 变为：
δW=F·vdt =Fvvdt
(2-15)
其中，Fv＝Fcos (F，v)，即仅沿速度方向的分力做功。当F与v垂直时，该力所做功为零，即不做功。
力所做的功将引起被作用质点动能的改变，即：
由式(2-1)改写成m((dv)/(dt))=F，因dr=vdt，即：
此式与式(2-16)完全相同，其中1/2mv2为质点的动能。
若沿力F的轨迹曲线段M1M2积分，可得：
△T=W12 (2-17)
其中，动能增量△T=T2-T1，而T1＝1/2mv21，T2＝1/2mv22;力F由M1点至M2点所做的功W12＝ F·dr= Fcosθds，而θ为力F与轨迹切向矢量间的夹角，s为沿轨迹曲线的自然坐标。
式 (2-17)
...... （共3272字） [阅读本文]>>
物流运输包装设计根据牛顿第二定律，质点的加速度大小与它所受力的大小成正比，且方向一致(图2-1)，表达式为：ma=F(2-1)图2-1力和加速度若沿力矢F的方向取坐标轴OX，则力矢F和加速度矢a在X轴上的投影的标量表达
物流运输包装设计力F在t1到t2的时间间隔内的累积效应称为力F在此时间间隔内的冲量S，表示为：S=Fdt(2-7)式中Fdt——元冲量，N·S。冲量S将引起物体动量的改变，关系式为：S=△(mv)=mv2-mv1(2-
物流运输包装设计包装件由各种材料组成，为了弄清楚力和能量在其内部的传递、转换，必须对应力、应变及应变能等概念深入理解。1.静应力与动应力当一常力，如重力，作用于某一厚度的材料上时，承载面积设为A，可认为重力W均匀地施加
物流运输包装设计在物体受外力作用下内部产生阻止变形、企图恢复原来状态的力，即内部应力，而去掉外力时，随状态的恢复其内部应力也随之消失，这种内部应力就是弹性(恢复)力。如橡胶、发泡塑料、弹簧等缓冲包装材料在力的作用下发生
物流运输包装设计固体在其弹性极限内对外力有弹性表现，但超过该界限就会发生流动，以致造成永久变形或破坏，该现象与液体流动是不相同的，称这种性质为塑性。在应力-应变曲线上，当加载范围在弹性极限以下，在直线段上卸载时，可沿原
上一篇