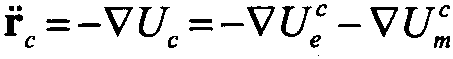这一节利用高斯摄动方程推导了经典平均轨道要素差与其一阶导的关系，在推导过程中做如下假设： 主从卫星间的相对距离远小于主卫星到地心的距离，在这个假设下对高斯摄动方程做线性化处理得到δ，详细推导过程如下。
在本节所考虑的二星系统中主卫星不受控制力，从卫星受到控制力的作用。因此，根据高斯摄动方程，主卫星轨道要素的变化率在J2摄动下可表示为：
＝a(e)
(5.40)
从卫星可表示为：
j＝a(ej)+B(ej)u
(5.41)
式中，u=(ux，uy，uz)T为沿主卫星LVLH坐标系3个坐标轴的控制向量，矩阵a(e)为：
矩阵B (e)表示为：
根据式 (5.4)可得如下关系式：
δ＝j-
(5.44)
将式(5.40)和式(5.41)代入到式(5.44)可得：
δ＝a(ej)-a(e)+ ...... （共540字） [阅读本文]>>
长寿卫星编队飞行理论我们在以前的研究中提出了用6个参考卫星轨道要素 (RSV)来描述参考卫星的地球轨道运动。这6个轨道要素是： 卫星到地心的距离及其变化率(r，vx)，轨道倾角i，纬度幅角θ，轨道角动量h和升交点赤经Ω。
长寿卫星编队飞行理论图4.1中的任意向量r在LVLH坐标系(S0-xyz)和地心坐标系(E-XYZ)表述分别为r和rE，它们的关系为r=TrE (4.1)式中，T为从地心坐标系到LVLH坐标系的旋转变换，由于参考卫星S0
长寿卫星编队飞行理论目前，国外研究的重点在于对Hill方程或者改进的Hill方程进行细致的摄动影响分析，并取得了很好的成果; 国内张玉锟研究了编队卫星的动力学和运动学设计方法，并以此为基础进行了大量的摄动分析研究，但对于
长寿卫星编队飞行理论在上一节中，在临界倾角处利用“严格J2不变轨道”条件，卫星的自然周期类圆形卫星编队已经被设计提出，并且通过STK高精度仿真，得到了很好的效果，证明设计是非常准确的。但是由于“严格J2不变轨道”条件约束
长寿卫星编队飞行理论本章设计了一种能够顺从J2摄动的自然周期类圆形编队作为卫星编队的目标轨道，并且本课题设计的目标轨道是以约束方程表述的、且独立于终端时刻，构造了终端时刻自由的最省燃料控制问题。9.1.1 相对运动方程考
上一篇