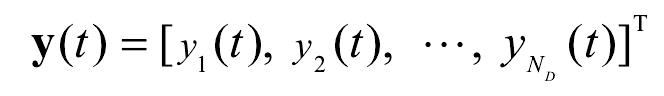
结构动力学中还采用广义特征值分析对式(2-65)的微分方程组解耦，称为模态(振型)分解法。式(2-65)的频率方程为，
式(2-101)的 ND个正实根 ωnj(j = 1，2，…，ND)为刚度矩阵 K 相对于质量矩阵 M 的广义特征值的平方根，称为结构的自振频率。相应地，对于第 j 阶自振频率，有特征方程(j = 1，2，…，ND)，
可得到广义特征向量 φj(j = 1，2，…，ND)即为对应于自振频率 ωnj的模态(振型)向量(ND×1)。将模态向量按列组装，称为模态(振型)矩阵(ND× ND)。
利用模态矩阵 Φ 对位移x(t)进行坐标转换，
式中，为模态响应时程向量(ND×1)，由各阶模态响应时程 yj(t)(j = 1，2，…，ND)组成。
将质量、刚度矩阵对角化，得到广义质量 ...... （共1948字） [阅读本文]>>
高耸烟囱结构抗风设计与风振控制由于风的随机性，脉动风速三分量 u(t)，v(t)，w(t)均为随机过程，一般可假定成均值为零的平稳随机过程，其均方根值分别为 σu，σv，σw。分别采用顺风向、横风向和竖向的湍流强度(Turbule
高耸烟囱结构抗风设计与风振控制大气边界层的自然风为湍流风，在微观气象尺度范围内，由于气流的不稳定性，其随机周期的变化范围从零点几秒到几分钟不等。对于高度 z(m)处的顺风向湍流风速 u(z，t)(m/s)，其频率的概率分布可通过无
高耸烟囱结构抗风设计与风振控制20 世纪 60 年代，Davenport [119]基于结构附近未扰动风的湍流特征提出了位于大气边界层内结构的脉动风荷载模型，对于微面或点状结构，基于拟定常假设式中，Cp为风压系数;该假设将来流全脉
高耸烟囱结构抗风设计与风振控制借鉴风速谱模型式(2-20)，将无量纲谱表达为如下形式：式中，为无量纲风荷载谱， Sp(f) 为单边风荷载谱(N2·s)， f 为频率(Hz)，为脉动风荷载总能量(方差 N2)，为无量纲频率，f0
高耸烟囱结构抗风设计与风振控制自功率谱参数 Sm、Fm、κ 可根据 S-F曲线，由式(2-49)至式(2-51)获得。式中，为离散的无量纲频率，Nfft为傅里叶变换长度，为奈奎斯特(Nyquist)频率，，γJ 为大于 1 的松弛
上一篇