1.1 引言
本节将介绍本书所研究问题的历史发展和意义.H-矩阵的定义是A.M.Ostrowski于1937年首先给出的[3,4],现在H-矩阵的最直观定义是其比较矩阵为M-矩阵[5]. 实际上,M-矩阵类是H-矩...查看详细>>
3620字5图1.2 研究工作
本书研究H-矩阵的判定问题. 作为应用,研究几类特殊H-矩阵Schur补的对角占优度及特征值分布区域. 然后,对H-矩阵的高阶推广——H-张量的正定性判定问题进行研究和探索. 全文共分五章,除概述和总...查看详细>>
531字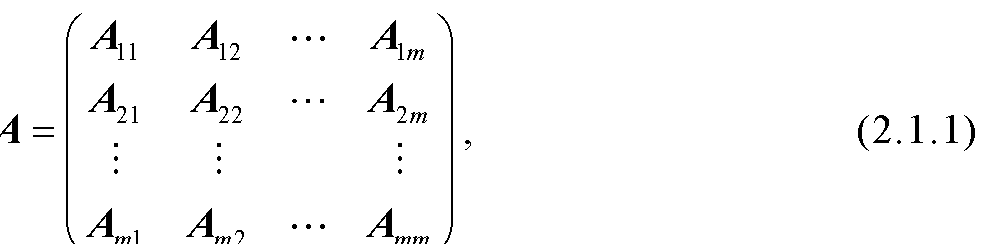
2.1 定义与性质
下面介绍几类重要的特殊H-矩阵.定义2.1设矩阵A=(aij)∈Cn×n,N={1,2,…,n},记Ri(A)=|aij|,Ci (A)=|aij|,若对任意i,j∈N,i≠j,(ⅰ)|aii|>...查看详细>>
2054字12图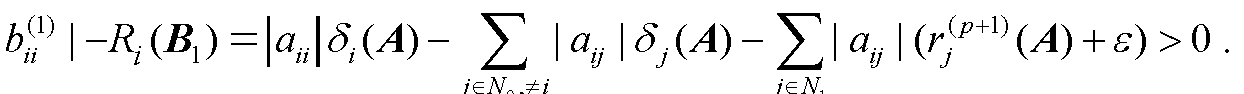
2.2 H-矩阵的一种构造判别法
本节通过递进选取对角矩阵因子元素,得到H-矩阵的一些新的判定方法,再进一步将此类判定方法推广到不可约矩阵和具有非零元素链矩阵的情形,并用实例说明这些方法的有效性.为了叙述方便,先引入下列记号: 设A=...查看详细>>
1719字1图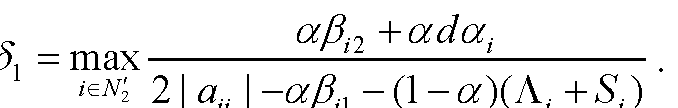
2.3 H-矩阵的实用新判据
引进下述记号:设N1,N2N, N1∪N2=N, N1∩N2=∅, α∈(0,1],...查看详细>>
1410字1图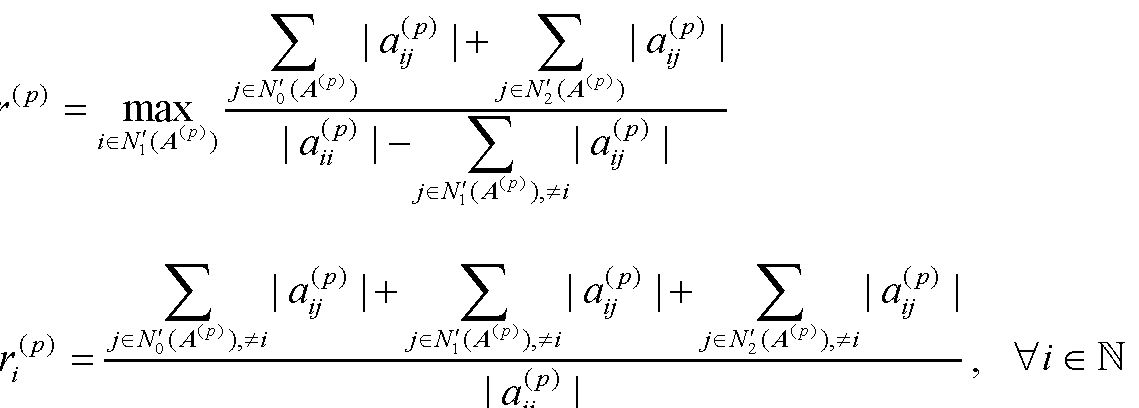
2.4 H-矩阵的迭代判别算法
H-矩阵的构造判别法就是构造一个正对角矩阵X,再把它右乘到需要判定的矩阵上,如果乘积矩阵是严格对角占优矩阵,则判别成功. 这样的判别过程从矩阵理论上来说比较简洁方便,但实际可操作性并不强,特别是对大型...查看详细>>
4563字1图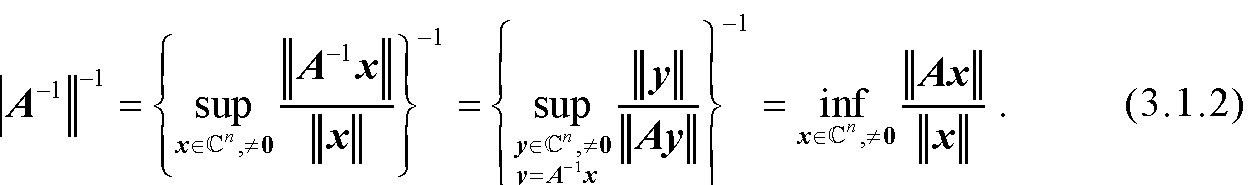
3.1 定义与性质
设A=(aij)∈Cn×n,如果βN,用|β|表示集合β的基数.对于非空集合β,γN,用A(β,γ)表示A中行指标位于β内、列指标位于γ内的子矩阵,其中子矩阵A(β,β...查看详细>>
2108字3图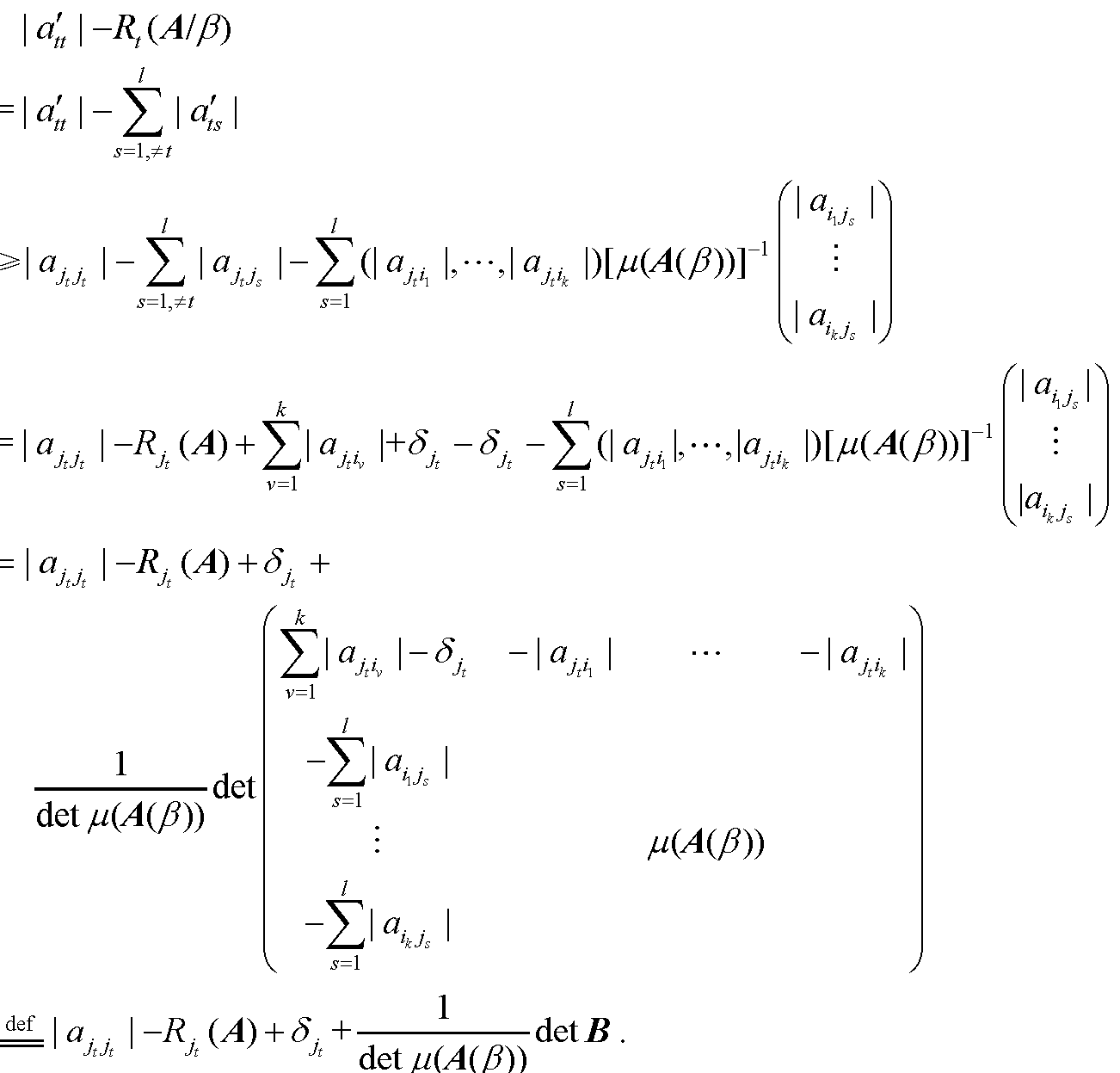
3.2 矩阵Schur补的对角占优度及特征值分布
本节研究一般矩阵Schur补的对角占优度,并利用不等式放缩技巧、Gersgorin圆盘定理和Ostrowski圆盘定理,用原矩阵的元素给出了相应矩阵Schur补的特征值分布区域.3.2.1 矩阵Sch...查看详细>>
1788字1图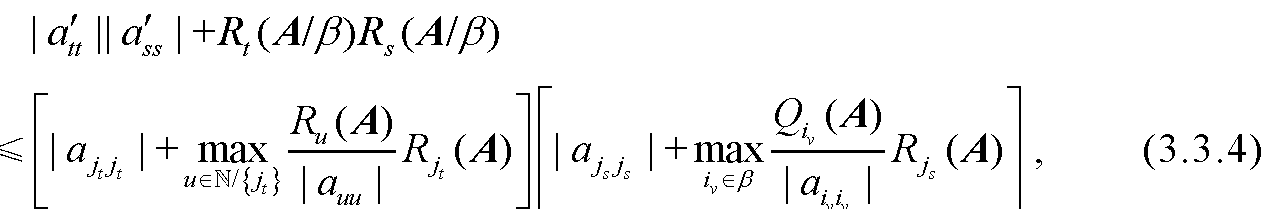
3.3 Ostrowski矩阵Schur补的对角占优度及特征值分布
本节研究H-矩阵的子类——Ostrowski矩阵Schur补的对角占优度,并利用不等式放缩技巧和Brauer卵形定理,用原矩阵的元素给出相应矩阵Schur补的特征值分布区域.3.3.1 Ostrows...查看详细>>
2444字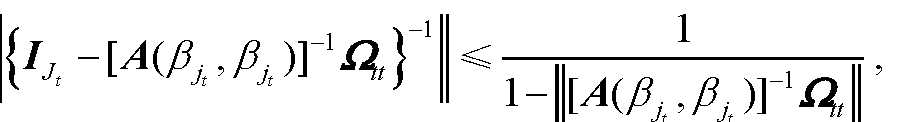
3.4 块对角占优矩阵Schur补的对角占优度及特征值分布
本节研究块H-矩阵——Ⅰ (Ⅱ)-块严格 (双) 对角占优矩阵Schur补的块对角占优度,得到了Ⅰ (Ⅱ)-块严格 (双) 对角占优矩阵Schur补的每一块对角占优程度要优于原来的块矩阵的相应块行的对...查看详细>>
3319字
